

解:(1)AB=AC说理如下:
∵EC平分∠AED,DB平分∠ADE,
∴∠AEC= ∠AED,∠ADB=
∠AED,∠ADB= ∠ADE.
∠ADE.
∵∠AED=∠ADE,
∴∠AEC=∠ADB.
在△AEC和△ADB中,∠AEC=∠ADB,AE=AD,∠A=∠A,
∴△AEC≌△ADB(ASA)
∴AB=AC;
(2)BE=CD,BE⊥CD
∵∠EAD=∠BAC,
∴∠EAD+∠BAD=∠BAC+∠BAD,
∴∠EAB=∠DAC,
在△AEB和△ADC中,
AB=AC
∠EAB=∠DAC
AE=AD
∴△AEB≌△ADC(SAS),
∴∠AEB=∠ADC,
∵∠AEB+∠DEB+∠ADE=90°,
∴∠ADC+∠DEB+∠ADE=90°①,
∵∠ADC+∠DEB+∠ADE+∠DOE=180°②,
②﹣①得,
∠DOE=90°,
∴BE⊥CD。


科目:初中数学 来源: 题型:
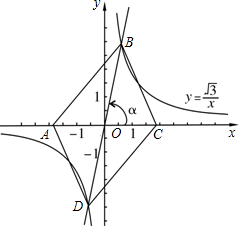 我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数y=
我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数y=
| ||
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 图2的位置,AD、BE相交于O,请你判断线段BE与CD的关系,并说明理由.
图2的位置,AD、BE相交于O,请你判断线段BE与CD的关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 图2的位置,AD、BE相交于O,请你判断线段BE与CD的关系,并说明理由.
图2的位置,AD、BE相交于O,请你判断线段BE与CD的关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com