
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= ![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ![]() ,OB=4,OE=2.
,OB=4,OE=2. 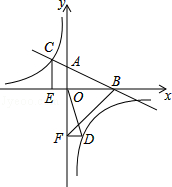
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
【答案】
(1)解:∵OB=4,OE=2,
∴BE=OB+OE=6.
∵CE⊥x轴,
∴∠CEB=90°.
在Rt△BEC中,∠CEB=90°,BE=6,tan∠ABO= ![]() ,
,
∴CE=BEtan∠ABO=6× ![]() =3,
=3,
结合函数图象可知点C的坐标为(﹣2,3).
∵点C在反比例函数y= ![]() 的图象上,
的图象上,
∴m=﹣2×3=﹣6,
∴反比例函数的解析式为y=﹣ ![]() .
.
(2)解:∵点D在反比例函数y=﹣ ![]() 第四象限的图象上,
第四象限的图象上,
∴设点D的坐标为(n,﹣ ![]() )(n>0).
)(n>0).
在Rt△AOB中,∠AOB=90°,OB=4,tan∠ABO= ![]() ,
,
∴OA=OBtan∠ABO=4× ![]() =2.
=2.
∵S△BAF= ![]() AFOB=
AFOB= ![]() (OA+OF)OB=
(OA+OF)OB= ![]() (2+
(2+ ![]() )×4=4+
)×4=4+ ![]() .
.
∵点D在反比例函数y=﹣ ![]() 第四象限的图象上,
第四象限的图象上,
∴S△DFO= ![]() ×|﹣6|=3.
×|﹣6|=3.
∵S△BAF=4S△DFO,
∴4+ ![]() =4×3,
=4×3,
解得:n= ![]() ,
,
经验证,n= ![]() 是分式方程4+
是分式方程4+ ![]() =4×3的解,
=4×3的解,
∴点D的坐标为( ![]() ,﹣4).
,﹣4).
【解析】(1)由边的关系可得出BE=6,通过解直角三角形可得出CE=3,结合函数图象即可得出点C的坐标,再根据点C的坐标利用反比例函数图象上点的坐标特征,即可求出反比例函数系数m,由此即可得出结论;(2)由点D在反比例函数在第四象限的图象上,设出点D的坐标为(n,﹣ ![]() )(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF , 根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.
)(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF , 根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.


科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)= ![]() .如:12=1×12=2×6=3×4,则F(12)=
.如:12=1×12=2×6=3×4,则F(12)= ![]() .则在以下结论:
.则在以下结论:
①F(5)=5;②F(24)= ![]() ;
;
③若a是一个完全平方数,则F(a)=1;
④若a是一个完全立方数,即a=x3(x是正整数),
则F(a)=x.则正确的结论有________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由半圆和长方形构成,长方形的长BC为8m,宽AB为1m,该隧道内设双向行驶的车道(共有2条车道),若现有一辆货运卡车高4m,宽2.3m。则这辆货运卡车能否通过该隧道?说明理由.
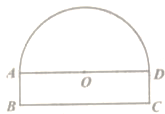
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= ![]() AB中,一定正确的是( )
AB中,一定正确的是( ) 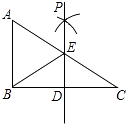
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.
(1)求该函数的解析式,并画出它的图象;
(2)如果这条直线经过点P(m,2),求m的值;
(3)若O为坐标原点,求直线OP的解析式;
(4)求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
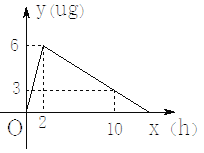
【题目】某医药研究生开发了一种新药,在实验药效时发现,如果成人按规剂量服用,那么服用药后2h时血液中含药量最高,达每毫升6ug,接着逐步衰减,10h时血液中含药量每毫升3ug,每毫升血液中含药量y(ug)随时间x(h)的变化如图所示,当成人按规定剂量服药后.
(1)分别求出x≤2和x>2时,y与x之间的函数关系式;
(2)如果每毫升血液含药量为4ug或4ug以上时在治疗疾病时是有效的,那么这个有效时间是多长?每天至少吃几次药疗效最好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题:
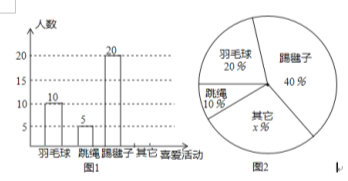
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据 ②图2中x= .
(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中,点 G 是边 CD 上一点(不与端点 C,D 重合),以 CG为边在正方形 ABCD 外作正方形 CEFG,且 B、C、E 三点在同一直线上,设正方形 ABCD 和正方形 CEFG 的边长分别为 a 和 b.
(1)分别用含 a,b 的代数式表示图 1 和图 2 中阴影部分的面积 S1、S2;
(2)如果 a+b=5,ab=3,求 S1 的值;
(3)当 S1<S2 时,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com