
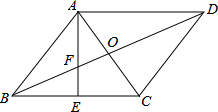
 如图,?ABCD的对角线AC和BD相交于点O,AE垂直平分BC,分别交BD、BC于点F、E,已知sin∠BAE=
如图,?ABCD的对角线AC和BD相交于点O,AE垂直平分BC,分别交BD、BC于点F、E,已知sin∠BAE= .
. 的值;
的值; =
= ,
, =
= =
= ;
; AC=5,
AC=5, =8,
=8, =
= =2,
=2, AF,
AF, AF+AF=AE=8,
AF+AF=AE=8, .
. =
= ,设BE=3x,则AB=5x,CE=3x,然后根据平行四边形的性质得AD=6x,再计算
,设BE=3x,则AB=5x,CE=3x,然后根据平行四边形的性质得AD=6x,再计算 ;
; AC=5,利用勾股定理计算出BE=8,由AD∥BC得到△ADF∽△EBF,利用相似可得到EF=
AC=5,利用勾股定理计算出BE=8,由AD∥BC得到△ADF∽△EBF,利用相似可得到EF= AF,然后利用EF+AF=AE=8计算即可求出AF.
AF,然后利用EF+AF=AE=8计算即可求出AF.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com