
 如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为
如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为| 1 |
| 2 |
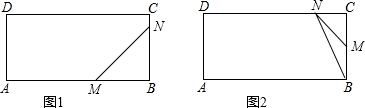 解:①如图1,点M在AB上,点N在BC上时,t<4,BM=10-2t,BN=t,
解:①如图1,点M在AB上,点N在BC上时,t<4,BM=10-2t,BN=t,| 10 |
| 3 |
| 2 |
| 2 |
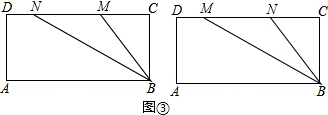
| 17 |
| 3 |
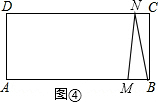
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 10 |
| 3 |
| 2 |
| 9 |
| 2 |
| 10 |
| 3 |
| 2 |
| 9 |
| 2 |


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
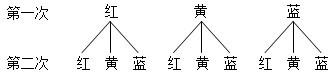
| A、随机摸出一个球后放回,再随机摸出1个球 |
| B、随机摸出一个球后不放回,再随机摸出1个球 |
| C、随机摸出一个球后放回,再随机摸出3个球 |
| D、随机摸出一个球后不放回,再随机摸出3个球 |
查看答案和解析>>
科目:初中数学 来源: 题型:
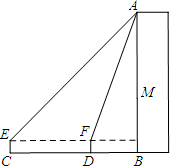 黄冈市高效课堂现场会在英山实验中学召开,为营造氛围,举办方从教学楼顶端A点处向下悬挂“优化教学方法,构建高效课堂”大型标语.九年级学生王港用高1m的测角仪在地面C点测得楼顶A点的仰角为45°,沿CB方向前进15m到达D点,测得A点仰角的正切值为
黄冈市高效课堂现场会在英山实验中学召开,为营造氛围,举办方从教学楼顶端A点处向下悬挂“优化教学方法,构建高效课堂”大型标语.九年级学生王港用高1m的测角仪在地面C点测得楼顶A点的仰角为45°,沿CB方向前进15m到达D点,测得A点仰角的正切值为| 8 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、-2(a2-4ab+4b2) |
| B、-2(a-2b)2 |
| C、-2(a+2b)2 |
| D、2(a-2b)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com