
【题目】如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=°. 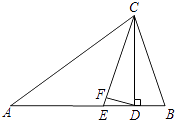
【答案】70
【解析】解:∵∠A+∠B+∠ACB=180°,∠A=30°,∠B=70°, ∴∠ACB=80°,
∵CE平分∠ACB,
∴∠BCE= ![]() ∠ACB=
∠ACB= ![]() ×80°=40°,
×80°=40°,
∵CD⊥AB,
∴∠CDB=90°,
∵∠B=70°,
∴∠BCD=90°﹣70°=20°,
∴∠FCD=∠BCE﹣∠BCD=20°,
∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF=90°﹣∠FCD=70°.
所以答案是:70.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


科目:初中数学 来源: 题型:
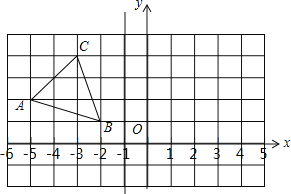
【题目】在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形上)
(1)画出△ABC关于直线l:x=﹣1的对称三角形△A1B1C1;并写出A1、B1、C1的坐标.
(2)在直线x=﹣l上找一点D,使BD+CD最小,满足条件的D点为 .
提示:直线x=﹣l是过点(﹣1,0)且垂直于x轴的直线.
查看答案和解析>>
科目:初中数学 来源: 题型:
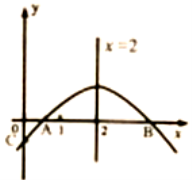
【题目】如图,二次函数y=ax2+bx+c (a≠0)的图像与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC. 则下列结论:
①abc>0 ②9a+3b+c<0 ③c>-1 ④关于x的方程ax2+bx+c=0 (a≠0)有一个根为-![]()
其中正确的结论个数有( )
A. 1个 B. 2个 C.3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
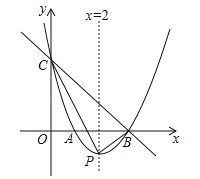
【题目】如图,直线y=﹣x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线![]() 与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.
(1)求该抛物线的解析式;
(2)连接PB、PC,求△PBC的面积;
(3)连接AC,在x轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( ) 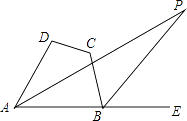
A.10°
B.20°
C.30°
D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( ) 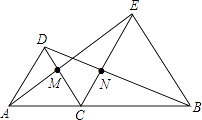
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,王明和李玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 . 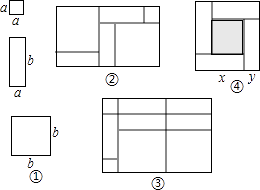
(1)图③可以解释为等式:
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图①所示的块,块,块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式: 1)xy= ![]() (2)x+y=m(3)x2﹣y2=mn(4)x2+y2=
(2)x+y=m(3)x2﹣y2=mn(4)x2+y2= ![]()
其中正确的有
A.1个
B.2个
C.3个
D.4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处,若△CDB′ 恰为等腰三角形,则DB′ 的长为 .
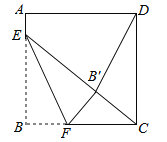
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com