【题目】下列是关于四个图案的描述.
图1所示是太极图，俗称“阴阳鱼”，该图案关于外圈大圆的圆心中心对称；
图2所示是一个正三角形内接于圆；
图3所示是一个正方形内接于圆；
图4所示是两个同心圆，其中小圆的半径是外圈大圆半径的三分之二.
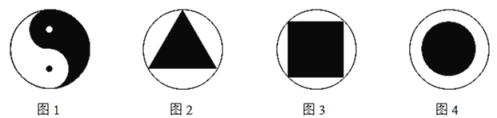
这四个图案中，阴影部分的面积不小于该图案外圈大圆面积一半的是（ ）
A.图1和图3B.图2和图3C.图2和图4D.图1和图4
【答案】A
【解析】
图(1)根据题意，结合图形，可用割补法直接求得结果．
图(2)先求出正三角形的中心角及边心距，再根据三角形的面积公式求解比较即可．
图(3) 根据圆内接正方形的性质，求出圆内正方形的面积比较即可.
图(4)求出小圆的面积比较.,
图(1)割补法就是把图形切开，把切下来的那部分移动到其他位置，使题目便于解答．运用割补法可以发现：阴影部分的面积正好是半圆的面积，即大圆面积的一半．
图(2)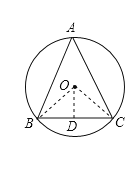 
如图所示,过O作OD⊥BC, 
=30°,OD=
OB=R,
由勾股定理和垂径定理得
BD=CD=
R, S
ABC=3 SBOC=3
（2R）R=
R2
R2 <
R2
图（3）
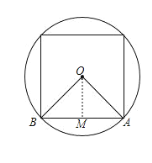
如图所示，正方形的面积=4
=
=2R2>
图4：
阴影部分小圆面积=
=
< ;
所以图1和图3符合要求
故选：A．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】将背面是质地、图案完全相同，正面分别标有数字-2，-1，1，2的四张卡片洗匀后，背面朝上放置在桌面上．随机抽取一张卡片，将抽取的第一张卡片上的数字作为横坐标，第二次再从剩余的三张卡片中随机抽取一张卡片，将抽取的第二张卡片上的数字作为纵坐标．
（1）请用列表法或画树状图法求出所有可能的点的坐标；
（2）求出点在x轴上方的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
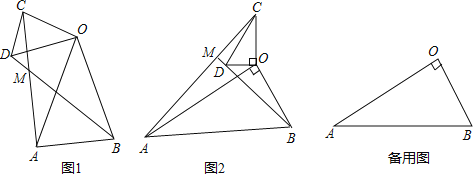
【题目】（1）问题发现
如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：
①
的值为 ；
②∠AMB的度数为 ．
（2）类比探究
如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M．请判断的值及∠AMB的度数，并说明理由；
（3）拓展延伸
在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB=
，请直接写出当点C与点M重合时AC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，E是AD的中点，延长CE，BA交于点F，连接AC，DF．
（1）求证：四边形ACDF是平行四边形；
（2）当CF平分∠BCD时，写出BC与CD的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为增强公民的节约意识，合理利用天然气费源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调能后的收费价格如表所示：
每月用气量 | 单价(元/m3) |
不超出75m3的部分 | 2 |
超出75 m3不超过125 m3的部分 | a |
超出125 m2的部分 | a＋0.5 |
(1)若某户3月份用气量为60 m3，则应交费多少元？
(2)调价后每月支付燃气费用y(元)与每月用气量x(m3)的函数关系如图所示，求a的值及线段AB对应的一次函数的表达式；
(3)求射线BC对应的一次函数的表达式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图
，在正方形
中，
平分
,交
于点
,过点
作
,交的延长线于点
,交
的延长线于点
,
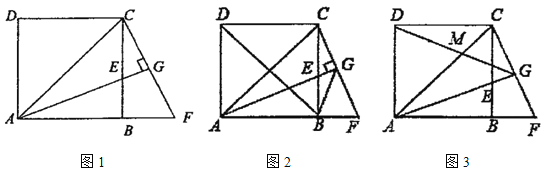
（1）求证:
;
（2）如图
，连接
、
,求证平分
;
（3）如图
,连接
交
于点
, 求
的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
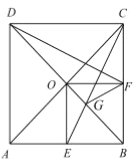
【题目】如图，在边长为1的正方形
中，对角线
，
相交于点
，点
，点
分别是
，
的中点，
交于点
，连接
，
，
，得到以下四个结论：①
，②
，③
，④
，其中正确的结论是________（填写序号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
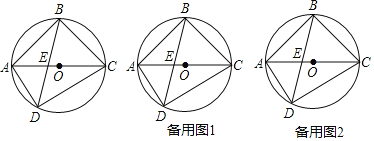
【题目】如图，四边形ABCD内接于⊙O，AC为直径，AC和BD交于点E，AB＝BC．
（1）求∠ADB的度数；
（2）过B作AD的平行线，交AC于F，试判断线段EA，CF，EF之间满足的等量关系，并说明理由；
（3）在（2）条件下过E，F分别作AB，BC的垂线，垂足分别为G，H，连接GH，交BO于M，若AG＝3，S四边形AGMO：S四边形CHMO＝8：9，求⊙O的半径．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
