练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．如过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图所示的几何体，其正确的展开图为（　　）
    A．B．C．D．

    分析 由平面图形的折叠及立体图形的表面展开图的特点解题．

    解答 解：选项A、C、D折叠后都不符合题意，只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点，与正方体三个剪去三角形交于一个顶点符合．
    故选：B．

    点评 考查了截一个几何体和几何体的展开图．解决此类问题，要充分考虑带有各种符号的面的特点及位置．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．如图所示，直线AB、CD相交于点O，OE⊥AB，OB平分∠DOF，若∠EOC=110°，求∠BOF，∠COF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．（1）如图1，在平行四边形ABCD中，将△BCD沿BD翻折，使点C落在点E处，BE和AD相交于点O．求证：OA=OE．
    （2）如图2，AB是⊙O的直径，AC是⊙O的弦，过点B作⊙O的切线DE，与AC的延长线交于点D，作AE⊥AC交DE于点E．求证：∠BAD=∠E．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列说法正确的是（　　）
    A．（3，2）和（2，3）表示同一个点B．点（$\sqrt{3}$，0）在x轴的正半轴上
    C．点（-2，4）在第四象限D．点（-3，1）到x轴的距离为3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

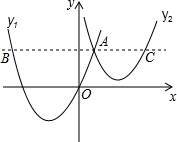    6．如图，抛物线y1=a（x+2）2+m过原点，与抛物线y2=$\frac{1}{2}$（x-3）2+n交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．下列结论：①两条抛物线的对称轴距离为5；②x=0时，y2=5；③当x＞3时，y1-y2＞0；④y轴是线段BC的中垂线．正确结论是①③④（填写正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列计算正确的是（　　）
    A．a3+a2=a5B．（a-b）2=a2-b2C．a6b÷a2=a3bD．（-ab3）2=a2b6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

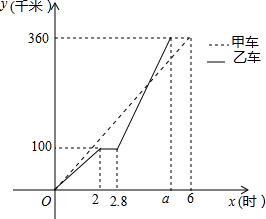    3．甲、乙两车同时从A地前往B地，乙行驶途中有一次停车修理，修好后乙车的行驶速度是原来的2倍，两车行驶路程y（千米）与行驶时间x（时）的函数图象如图所示，
    （1）求乙车到达B地所用的时间a的值；
    （2）行驶过程中，出发多长时间两车首次相遇？
    （3）当x=3时，求甲、乙两车之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．直线y=$\frac{1}{2}$x+b与函数y=x2+|2x2-1|的图象有且只有三个交点，则b的值为$\frac{1}{2}$+$\frac{\sqrt{2}}{4}$或1+$\frac{\sqrt{2}}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，抛物线y=a（x-2）2+h与x轴交于A（6，0）和B两点，与y轴交于点C（0，2$\sqrt{3}$），点M从点B出发以每秒2个单位的速度向点A运动，设运动时间为t秒，过点M作直线MP∥BC与线段AC交于点P，再以线段PM为斜边作Rt△PMN，点N在x轴上．

    （1）求抛物线的表达式；
    （2）求Rt△PMN的斜边PM的长（用含有t的代数式表示），并求当Rt△PMN的顶点P与AC的中点D重合时t的值；
    （3）在（2）的条件下，在△AOC的内部作矩形DEOF，点E，F分别在x轴和y轴上，设Rt△PMN和矩形DEOF重叠部分的面积为S，当运动时间在0≤t≤2范围内时，求出S与t之间的函数关系式，并求出S的最大值．

    查看答案和解析>>

    同步练习册答案