
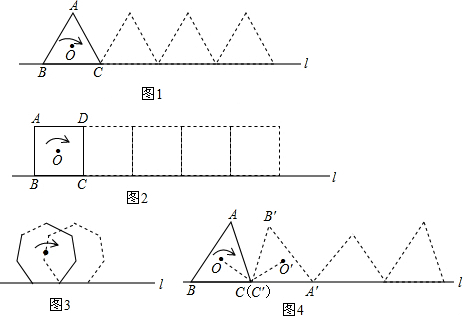
| 360° |
| n |
| 120πR |
| 180 |
| 90πR |
| 180 |
| 360° |
| n |
| ||
| 180 |
| (180-γ)πR |
| 180 |
| (180-α)πR |
| 180 |
| (180-β)πR |
| 180 |


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
| A、方程3x2-4=2x的二次项系数为3,一次项系数为-2,常数项为-4 |
| B、同一时刻在阳光照射下,物体越长,地面上的影子越长 |
| C、四个角都是直角的两个四边形一定相似 |
| D、某种彩票中奖的概率是1%,买100张该种彩票一定会中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,矩形ABCD的顶点,A的坐标为(1,0),对角线的交点P的坐标为(
如图,在直角坐标系中,矩形ABCD的顶点,A的坐标为(1,0),对角线的交点P的坐标为(| 5 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
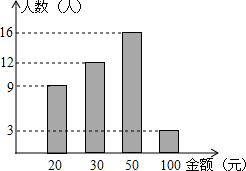 春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.
春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.查看答案和解析>>
科目:初中数学 来源: 题型:
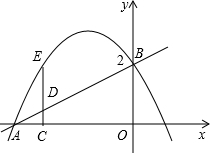 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com