解:(1)
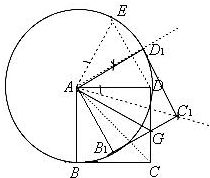
(2)连接AG,
∵AD=AB
1,AG=AG,
∴直角三角形AB
1G≌△ADG,
∵∠BAB
1=30°,
∴∠B
1AD=60°,
∴∠B
1AG=30°,
∵AB
1=a,
∴B
1G=

,
∴四边形AB
1GD=2×a×

÷2=
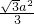
.
∴两正方形不重合部分的面积=2×(a
2-
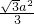
)=
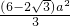
.
分析:(1)①以点A为圆心,AD长为半径作圆,再以点D为圆心,DA长为半径作弧,与圆的交点为E,连接AE,DE,△ADE就是一个等边三角形.∠EAD=60°;
②作∠EAD的角平分线,得到一个30°的角,角平分线与圆的交点为D
1;
③连接AC,以AC为一边根据②中30度的角作∠CAC1=30°,以点A为圆心,AC长为半径画弧与角的另一边交点为C
1;
④以AB为一边,作∠BAB
1等于已知角30度,与圆的交点为B
1.
顺次连接AB
1C
1D
1,正方形AB
1C
1D
1就是所求的正方形.
(2)从图中可以发现两正方形不重合部分的面积,就是正方形的面积减四边形AB
1GD的面积.连接AG,求它的面积.根据面积公式计算.
点评:(1)题的难点在于作一个30°的角,作出30°的角后,旋转变换根据这个角度找对应点就可以了.
(2)题的关键是根据勾股定理计算重合部分的面积,然后得出不重合部分的面积.

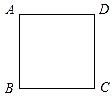 如图,已知边长为a的正方形ABCD.
如图,已知边长为a的正方形ABCD.
 ,
, ÷2=
÷2=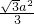 .
.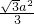 )=
)=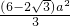 .
.

 金博士一点全通系列答案
金博士一点全通系列答案 如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH,则下列结论正确的是( )
如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH,则下列结论正确的是( )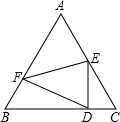 如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )
如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )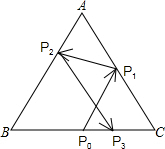 如图,已知边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角),且1<BP3<
如图,已知边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角),且1<BP3< 用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )
用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )