
| A. | $\frac{20}{21}$ | B. | $\frac{61}{84}$ | C. | $\frac{589}{840}$ | D. | $\frac{431}{760}$ |
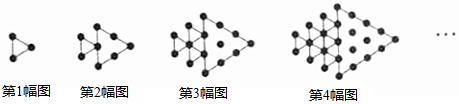
分析 首先根据图形中“●”的个数得出数字变化规律,进而求出即可.
解答 解:a1=3=1×3,a2=8=2×4,a3=15=3×5,a4=24=4×6,…,an=n(n+2);
∴$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{19}}$=$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+$\frac{1}{4×6}$+…+$\frac{1}{19×21}$=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{19}$-$\frac{1}{21}$)=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{20}$-$\frac{1}{21}$)=$\frac{589}{840}$,
故选C.
点评 此题考查图形的变化规律,找出图形之间的联系,找出规律解决问题.


科目:初中数学 来源: 题型:解答题
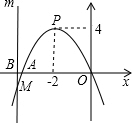 如图,已知抛物线l1的顶点是P(-2,4),且经过点O(0,0)、A(t,0),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.
如图,已知抛物线l1的顶点是P(-2,4),且经过点O(0,0)、A(t,0),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
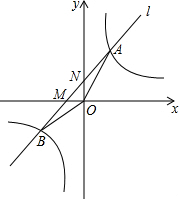 如图,设反比例函数的解析式为y=$\frac{3k}{x}$(k>0).
如图,设反比例函数的解析式为y=$\frac{3k}{x}$(k>0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{240}{x-20}$-$\frac{120}{x}$=4 | B. | $\frac{240}{x+20}$-$\frac{120}{x}$=4 | C. | $\frac{120}{x}$-$\frac{240}{x-20}$=4 | D. | $\frac{120}{x}$-$\frac{240}{x+20}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
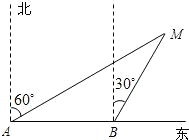 如图,某渔船上的渔民在A处测得灯塔M在北偏东60°方向,这艘渔船以20海里/小时的速度向正东方向航行,半小时到达B点.在B处测得灯塔M在北偏东30°方向,问B处与灯塔M的距离是多少海里?
如图,某渔船上的渔民在A处测得灯塔M在北偏东60°方向,这艘渔船以20海里/小时的速度向正东方向航行,半小时到达B点.在B处测得灯塔M在北偏东30°方向,问B处与灯塔M的距离是多少海里?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com