
已知⊙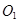 、⊙
、⊙ 外切于点
外切于点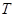 ,经过点
,经过点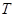 的任一直线分别与⊙
的任一直线分别与⊙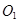 、⊙
、⊙ 交于点
交于点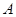 、
、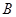 ,
,
(1)若⊙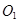 、⊙
、⊙ 是等圆(如图1),求证
是等圆(如图1),求证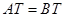 ;
;
(2)若⊙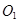 、⊙
、⊙ 的半径分别为
的半径分别为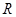 、
、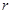 (如图2),试写出线段
(如图2),试写出线段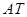 、
、 与
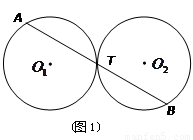
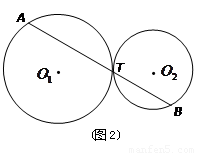
与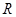 、
、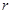 之间始终存在的数量关系(不需要证明).
之间始终存在的数量关系(不需要证明).
解:(1)联结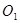
 .
.
∵⊙ .⊙
.⊙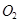 外切于点
外切于点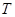 ,∴点T在
,∴点T在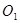
 上.
上.
如图,过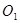 .
. 分别作
分别作 .
. ,垂足为
,垂足为 、
、 ,
,

∴ 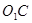 ∥
∥ .
.
∴
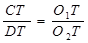 .
.
∵⊙ .⊙
.⊙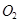 是等圆,∴
是等圆,∴ .
.
∴ ,
,
∴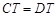 .
.
在⊙ 中,
中,
∵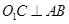 ,
,
∴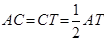 .
.
同理  .
.
∴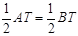 ,即
,即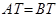 .
.
(2)线段 .
. 与
与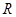 、
、 之间始终存在的数量关系是
之间始终存在的数量关系是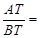
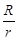 .
.
【解析】(1)连接O1O2,如图1所示,根据两圆外切时,两圆心连线过切点,得到O1O2过T点,由垂直得到一对直角相等,再由对顶角相等,利用两对对应角相等的两三角形相似得到△O1CT与△O2DT,由相似得比例,又两圆为等圆,半径相等可得出,可得出CT=DT,又O1C⊥AT,利用垂径定理得到CT等于AT的一半,同理DT等于BT的一半,等量代换可得出AT=BT,得证;
(2)线段AT、BT与R、r之间始终存在的数量关系是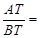
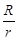 ,理由为:连接O1O2,如图2所示,根据两圆外切时,两圆心连线过切点,得到O1O2过T点,由垂直得到一对直角相等,再由对顶角相等,利用两对对应角相等的两三角形相似得到△O1CT与△O2DT,由相似得比例,将O1T=R,O2T=r代入,得到CT与DT的比值为R:r,又O1C⊥AT,利用垂径定理得到CT等于AT的一半,同理DT等于BT的一半,等量代换可得出AT与BT的比值为R:r.
,理由为:连接O1O2,如图2所示,根据两圆外切时,两圆心连线过切点,得到O1O2过T点,由垂直得到一对直角相等,再由对顶角相等,利用两对对应角相等的两三角形相似得到△O1CT与△O2DT,由相似得比例,将O1T=R,O2T=r代入,得到CT与DT的比值为R:r,又O1C⊥AT,利用垂径定理得到CT等于AT的一半,同理DT等于BT的一半,等量代换可得出AT与BT的比值为R:r.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
A、4
| ||
B、
| ||
C、2
| ||
| D、2Rr |
查看答案和解析>>
科目:初中数学 来源: 题型:
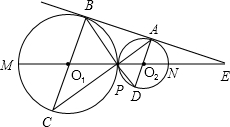 长线交⊙O1于C点,BP的延长线交⊙O2于D点,直线O1O2交⊙O1于M,交⊙O2于N,与BA的延长线交于点E.
长线交⊙O1于C点,BP的延长线交⊙O2于D点,直线O1O2交⊙O1于M,交⊙O2于N,与BA的延长线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
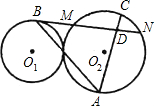 如图,已知⊙O1、⊙O2外切于点P,过P点的直线分别交⊙O1、⊙O2于B、A,⊙O1的切线BN交⊙O2于M、N,AC为⊙O2的弦,AC交MN于D,若AP=3,BP=2,则AD•AC=( )
如图,已知⊙O1、⊙O2外切于点P,过P点的直线分别交⊙O1、⊙O2于B、A,⊙O1的切线BN交⊙O2于M、N,AC为⊙O2的弦,AC交MN于D,若AP=3,BP=2,则AD•AC=( )| A、6 | B、15 | C、10 | D、12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1997•陕西)如图,已知⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,若⊙O1的半径为1,⊙O2的半径为3,则图中阴影部分的面积是( )
(1997•陕西)如图,已知⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,若⊙O1的半径为1,⊙O2的半径为3,则图中阴影部分的面积是( )查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com