【题目】如图， 
为线段
上一动点，分别过点
、
作
， 
，连接
、
，已知
， 
， 
，设
．
（1）用含
的代数式表示
的长；
（2）请问点
在什么位置时， 
的值最小，求出这个最小值；
（3）根据（2）中的规律和结论，构图求出代数式
的最小值．
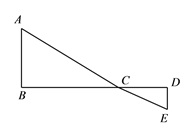
【答案】（1）用含x的代数式表示
的长
（2）当A、C、E三点共线时
取最小值，最小值为10；
（3）代数式最小值为
【解析】试题分析：
试题分析：（1）由于△ABC和△CDE都是直角三角形，故AC，CE可由勾股定理求得；
（2）若点C不在AE的连线上，根据三角形中任意两边之和＞第三边知，AC+CE＞AE，故当A、C、E三点共线时，AC+CE的值最小；
（3）由（1）（2）的结果可作BD=12，过点B作AB⊥BD，过点D作ED⊥BD，使AB=2，ED=3，连接AE交BD于点C，则AE的长即为代数式
+
的最小值，然后构造矩形AFDB，Rt△AFE，利用矩形的直角三角形的性质可求得AE的值．
试题解析：（1）由勾股定理知
∴
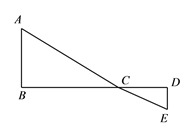
（2）当
、
、
三点共线时
取最小值，如下图
∴在
和
中
∴
∴
∴
∴
∴
∴
∴
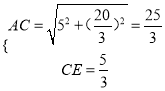
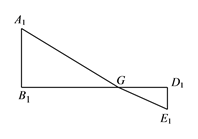
（3）根据（2）中规律可以构造出如图所示
由（2）中方法可得： 
∴
∴
∴
∴
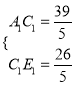
∴代数式最小值为
超能学典应用题题卡系列答案科目：初中数学 来源： 题型：
【题目】为加强中小学生安全和禁毒教育，某校组织了“防溺水、交通安全、禁毒”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同，每个篮球的价格相同)，购买1个足球和1个篮球共需159元；足球单价是篮球单价的2倍少9元．
(1)求足球和篮球的单价各是多少元；
(2)根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，学校最多可以购买多少个足球？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在下列条件中，①∠A+∠B=∠C； ②∠A：∠B：∠C=1：2：3； ③∠A=
∠B=
∠C；
④∠A=∠B=2∠C； ⑤∠A=2∠B=3∠C，能确定△ABC为直角三角形的条件有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．
（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （ ）
A. AB＝AC B. BD＝CD C. ∠B＝∠C D. ∠BDA＝∠CDA
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
