
已知AB和CD分别是半圆O的直径和弦,AD和BC的夹角为a,则S△CDE: S△ABE等于( ) 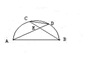
| A.Sin2a | B.cos2a | C.tan2a | D. sina |
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:学习周报 数学 北师大九年级版 2009-2010学年 第10期 总第166期 北师大版 题型:068
如图,已知AB和CD分别是直立在地面上的两根柱子,某一时刻,AB在阳光下的投影为BE,请你画出此时CD在阳光下的投影.

查看答案和解析>>
科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第20期 总第176期 沪科版 题型:068
如图,已知
AB和CD分别是直立在地面上的两根柱子,某一时刻AB在阳光下的投影为BE,请你画出此时CD在阳光下的投影.
查看答案和解析>>
科目:初中数学 来源:浙教版初一数学认识时间的可能性专项训练 题型:选择题
已知AB和CD分别是半圆O的直径和弦,AD和BC的夹角为a,则S△CDE: S△ABE等于( )
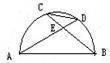
A、Sin2a B、cos2a C、tan2a D. sina
查看答案和解析>>
科目:初中数学 来源: 题型:
已知AB和CD分别是半圆O的直径和弦,AD和BC的夹角为a,则S△CDE: S△ABE等于( )

A、Sin2a B、cos2a C、tan2a D. sina
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com