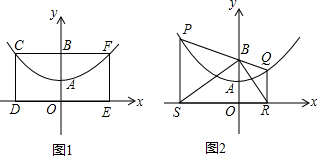
解:(1)方法一:∵F点坐标为(2,2),
∴EF=2,
∵矩形CDEF的面积为8,
∴CF=4,
∴点C的坐标为(-2,2),
设抛物线的解析式为y=ax
2+bx+c,其过三点A(0,1),C(-2,2),F(2,2),
所以,

,
解得

,
所以,此函数解析式为y=

x
2+1;
方法二:设抛物线的解析式为y=ax
2+c,其过点A(0,1)和F(2,2),
所以,
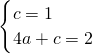
,
解得
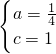
,
所以,此函数解析式为y=

x
2+1;
(2)①过点B作BN⊥PS于N,

∵P点在抛物线y=

x
2+1上,可设点P(a,

a
2+1),
∴PS=

a
2+1,OB=NS=2,BN=|a|,
∴PN=PS-NS=

a
2+1-2=

a
2-1,
在Rt△PNS中,PB
2=PN
2+BN
2=(

a
2-1)
2+(|a|)
2=(

a
2+1)
2,
∴PB=

a
2+1,
∵PS=

a
2+1,
∴PB=PS;
②方法一:设PS=b,QR=c,
由①知,PS=PB=b,QR=QB=c,PQ=b+c,
∴SR
2=(b+c)
2+(b-c)
2,
∴SR=2

,
假设存在点M,且MS=x,则MR=2

-x,
若使△PSM∽△MRQ,则有

=

,
即x
2-2

x+bc=0,
解得x
1=x
2=

,
∴SR=2

,
∴点M为SR的中点;
若使△PSM∽△QRM,则有

=

,
∴x=

,
∴

=

=

-1=

=
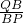
=

,
∴M点为原点O;
综上所述,点M为SR的中点时,△PSM∽△MRQ;点M为原点时△PSM∽△QRM;
方法二:若以P、S、R为顶点的三角形与以Q、M、R为顶点的三角形相似,
∵∠PSM=∠MRQ=90°,
∴分△PSM∽△MRQ和△PSM∽△QRM两种情况,
△PSM∽△MRQ时,∠SPM=∠RMQ,∠SMP=∠RQM,

根据直角三角形两锐角互余可得,∠PMS+∠SMR=90°,
∴∠PMQ=90°,
取PQ的中点N,连接MN,则MN=

PQ=

(QR+PS),
∴MN为梯形SRQP的中位线,
∴M为SR的中点;
△PSM∽△QRM时,

=

=
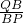
,
又∵
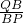
=

,
∴点M与点O重合,
综上所述,点M为SR的中点时,△PSM∽△MRQ;点M为原点时△PSM∽△QRM.
分析:(1)方法一:根据点F的坐标求出EF的长,再根据矩形的面积求出CF的长,然后求出点C的坐标,再设抛物线的解析式为y=ax
2+bx+c,然后利用待定系数法求二次函数解析式解答;
方法二:设抛物线的顶点式形式为y=ax
2+c,然后利用待定系数法求二次函数解析式解答即可;
(2)①过点B作BN⊥PS于N,根据点P在抛物线上设点P的坐标为(a,

a
2+1),然后表示出PS、OB、BN,再根据图形求出PN=PS-NS,在Rt△PNB中,利用勾股定理列式表示出PB
2,然后求出PB,从而得证;
②方法一:设PS=b,QB=c,利用勾股定理列式求出SR=2

,假设存在点M,且MS=x,表示出MR=2

-x,然后分△PSM和△MRQ相似,利用相似三角形对应边成比例列式求解即可得到点M为SR的中点;△PSM和△QRM相似时,利用相似三角形对应边成比例列式求解得到x=

,然后求出

=
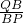
=

,从而得到点M与原点O重合;
方法二:根据∠PSM=∠MRQ=90°,分△PSM和△MRQ相似时,根据相似三角形对应角相等可得∠SPM=∠RMQ,∠SMP=∠RQM,再根直角三角形的性质求出∠PMQ=90°,取PQ的中点为N,连接MN,根据直角三角形斜边上的中线等于斜边的一半表示出MN=

PQ=

(QR+PS),从而判定MN为梯形SRQP的中位线,得到点M为SR的中点;△PSM和△QRM相似时,根据相似三角形对应边成比例可得

=

=
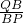
,再根据
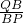
=

,可得点M与原点O重合.
点评:本题是二次函数综合题型,主要考查了二次函数的对称性,待定系数法求二次函数解析式,二次函数图象上点的坐标特征,勾股定理的应用,以及相似三角形对应边成比例的性质,综合性较强,难度较大,求点M的位置时要注意根据相似三角形对应边的不同分情况进行讨论.


 ,
, ,
, x2+1;
x2+1;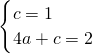 ,
,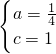 ,
, x2+1;
x2+1;
 x2+1上,可设点P(a,
x2+1上,可设点P(a, a2+1),
a2+1), a2+1,OB=NS=2,BN=|a|,
a2+1,OB=NS=2,BN=|a|, a2+1-2=
a2+1-2= a2-1,
a2-1, a2-1)2+(|a|)2=(
a2-1)2+(|a|)2=( a2+1)2,
a2+1)2, a2+1,
a2+1, a2+1,
a2+1, ,
, -x,
-x, =
= ,
, x+bc=0,
x+bc=0, ,
, ,
, =
= ,
, ,
, =
= =
= -1=
-1= =
=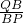 =
= ,
,
 PQ=
PQ= (QR+PS),
(QR+PS), =
= =
=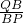 ,
,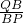 =
= ,
, a2+1),然后表示出PS、OB、BN,再根据图形求出PN=PS-NS,在Rt△PNB中,利用勾股定理列式表示出PB2,然后求出PB,从而得证;
a2+1),然后表示出PS、OB、BN,再根据图形求出PN=PS-NS,在Rt△PNB中,利用勾股定理列式表示出PB2,然后求出PB,从而得证; ,假设存在点M,且MS=x,表示出MR=2
,假设存在点M,且MS=x,表示出MR=2 -x,然后分△PSM和△MRQ相似,利用相似三角形对应边成比例列式求解即可得到点M为SR的中点;△PSM和△QRM相似时,利用相似三角形对应边成比例列式求解得到x=
-x,然后分△PSM和△MRQ相似,利用相似三角形对应边成比例列式求解即可得到点M为SR的中点;△PSM和△QRM相似时,利用相似三角形对应边成比例列式求解得到x= ,然后求出
,然后求出 =
=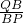 =
= ,从而得到点M与原点O重合;
,从而得到点M与原点O重合; PQ=
PQ= (QR+PS),从而判定MN为梯形SRQP的中位线,得到点M为SR的中点;△PSM和△QRM相似时,根据相似三角形对应边成比例可得
(QR+PS),从而判定MN为梯形SRQP的中位线,得到点M为SR的中点;△PSM和△QRM相似时,根据相似三角形对应边成比例可得 =
= =
=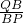 ,再根据
,再根据 =
= ,可得点M与原点O重合.
,可得点M与原点O重合.

 阅读快车系列答案
阅读快车系列答案

 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.