
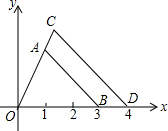
 已知A(1,2),B(3,0),将△AOB以坐标原点O为位似中心扩大到△OCD(如图),D(4,0),则点C的坐标为($\frac{4}{3}$,$\frac{8}{3}$).
已知A(1,2),B(3,0),将△AOB以坐标原点O为位似中心扩大到△OCD(如图),D(4,0),则点C的坐标为($\frac{4}{3}$,$\frac{8}{3}$).  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
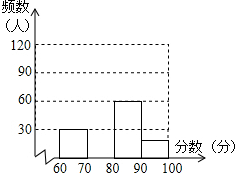 某中学举行了一次“奥运会”知识竞赛,赛后抽取部分参赛同学的成绩进行整理,并制作成图表如下:
某中学举行了一次“奥运会”知识竞赛,赛后抽取部分参赛同学的成绩进行整理,并制作成图表如下:| 分数段 | 频数 | 频率 |
| 第一组:60≤x<70 | 30 | 0.15 |
| 第二组:70≤x<80 | m | 0.45 |
| 第三组:80≤x<90 | 60 | n |
| 第四组:90≤x<100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com