
如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE的长.

解:(1)直线CD和⊙O的位置关系是相切,
理由是:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
即OD⊥CE,
∴直线CD是⊙O的切线,
即直线CD和⊙O的位置关系是相切;
(2)∵AC=2,⊙O的半径是3,
∴OC=2+3=5,OD=3,
在Rt△CDO中,由勾股定理得:CD=4,
∵CE切⊙O于D,EB切⊙O于B,
∴DE=EB,∠CBE=90°,
设DE=EB=x,
在Rt△CBE中,由勾股定理得:CE2=BE2+BC2,
则(4+x)2=x2+(5+3)2,
解得:x=6,
即BE=6.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
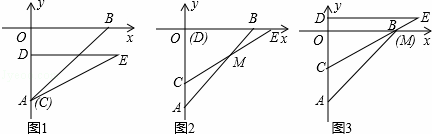
如图(1),在平面直角坐标系中,点A(0,﹣6),点B(6,0).Rt△CDE中,∠CDE=90°,CD=4,DE=4 ,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
(1)如图(2),当Rt△CDE运动到点D与点O重合时,设CE交AB于点M,求∠BME的度数.
(2)如图(3),在Rt△CDE的运动过程中,当CE经过点B时,求BC的长.
(3)在Rt△CDE的运动过程中,设AC=h,△OAB与△CDE的重叠部分的面积为S,请写出S与h之间的函数关系式,并求出面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
湘西盛产椪柑,春节期间,一外地运销客户安排15辆汽车装运A、B、C三种不同品质的椪柑120吨到外地销售,按计划15辆汽车都要装满且每辆汽车只能装同一种品质的椪柑,每种椪柑所用车辆部不少于3辆.
(1)设装运A种椪柑的车辆数为x辆,装运B种椪柑车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
| 椪柑品种 | A | B | C |
| 每辆汽车运载量 | 10 | 8 | 6 |
| 每吨椪柑获利(元) | 800 | 1200 | 1000 |
(2)在(1)条件下,求出该函数自变量x的取值范围,车辆的安排方案共有几种?请写出每种安排方案;
(3)为了减少椪柑积压,湘西州制定出台了促进椪柑销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销客户,按每吨50元的标准实行运费补贴.若要使该外地运销客户所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
一只不透明的袋子中装有两个完全相同的小球,上面分别标有1,2两个数字,若随机地从中摸出一个小球,记下号码后放回,再随机摸出一个小球,则两次摸出小球的号码之积为偶数的概率是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com