
【题目】直线y=﹣kx+k﹣3与直线y=kx在同一坐标系中的大致图象可能是( )
A.  B.
B.  C.
C.  D.
D. 
【答案】B
【解析】
若y=kx过第一、三象限,则k>0,所以y=-kx+k-3过第二、四象限,可对A、D进行判断;若y=kx过第二、四象限,则k<0,-k>0,k-3<0,所以y=-kx+k-3过第一、三象限,与y轴的交点在x轴下方,则可对B、C进行判断.
A、y=kx过第一、三象限,则k>0,所以y=-kx+k-3过第二、四象限,所以A选项错误;
B、y=kx过第二、四象限,则k<0,-k>0,k-3<0,所以y=-kx+k-3过第一、三象限,与y轴的交点在x轴下方,所以B选项正确;
C、y=kx过第二、四象限,则k<0,-k>0,k-3<0,所以y=-kx+k-3过第一、三象限,与y轴的交点在x轴下方,所以C选项错误;
D、y=kx过第一、三象限,则k>0,所以y=-kx+k-3过第二、四象限,所以D选项错误.
故选B.


科目:初中数学 来源: 题型:
【题目】已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣4,0),B点坐标为(6,0),点D为AC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.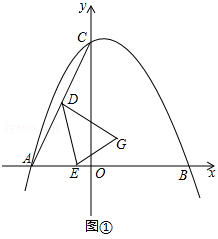
(1)求抛物线的解析式;
(2)如图①,将△ADE以DE为轴翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB、∠PCD的关系,请从你所得两个关系中选出任意一个,说明你探究的结论的正确性.

结论:(1)
(2)
选择结论: ,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=kx+2k交x轴于点A,交y轴正半轴于点B,且S△OAB=3
(1) 求A、B两点的坐标
(2) 将直线AB绕A点顺时针旋转45°,交y轴于点C,求直线AC的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( ) 
A.60
B.64
C.68
D.72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的发展,能源与环境已成为人们日益关注的问题.据统计,全球每年大约会产生近3亿吨的塑料垃圾(例如平时用的矿泉水瓶子等)和约5亿吨的废钢铁(例如平时扔掉的易拉罐等),某中学为了培养学生的环保意识,开展了“环境保护,从我做起”的主题活动,七(2)班同学在活动中积极响应,在甲小区设立了回收塑料瓶和易拉罐的两个垃圾桶,班长小明对2周的收集情况进行了统计,根据下列统计表和废品收购站的价格表,解决下列问题:


(1)全班2周共收集了 斤塑料瓶,收集了 斤易拉罐.
(2)班委会决定给贫困山区的孩子们捐赠一套价值50.4元的励志丛书,你认为按照这样的收集速度,至少需要收集几周才能实现这个愿望?写出计算过程.
(3)七(1)班在乙小区也设立了塑料瓶和易拉罐的回收点,两周收集塑料瓶和易拉罐共计440个,按相同价格出售后,所得金额比七(2)班两个周的废品回收金额多1.8元,求七(1)班同学两周收集的塑料瓶和易拉罐各多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com