
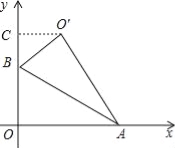
【题目】如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为(![]() ,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .

【答案】(![]() ,
,![]() )
)
【解析】
试题分析:作O′C⊥y轴于点C,首先根据点A,B的坐标分别为(![]() ,0),(0,1)得到∠BAO=30°,从而得出∠OBA=60°,然后根据Rt△AOB沿着AB对折得到Rt△AO′B,得到∠CBO′=60°,最后设BC=x,则OC′=
,0),(0,1)得到∠BAO=30°,从而得出∠OBA=60°,然后根据Rt△AOB沿着AB对折得到Rt△AO′B,得到∠CBO′=60°,最后设BC=x,则OC′=![]() x,利用勾股定理求得x的值即可求解.如图,作O′C⊥y轴于点C,
x,利用勾股定理求得x的值即可求解.如图,作O′C⊥y轴于点C,
∵点A,B的坐标分别为(![]() ,0),(0,1),∴OB=1,OA=
,0),(0,1),∴OB=1,OA=![]() ,∴tan∠BAO=
,∴tan∠BAO=![]() =
=![]() ,
,
∴∠BAO=30°,∴∠OBA=60°,∵Rt△AOB沿着AB对折得到Rt△AO′B,∴∠CBO′=60°,
∴设BC=x,则O′C=![]() x,∴x2+(
x,∴x2+(![]() x)2=1,解得:x=
x)2=1,解得:x=![]() (负值舍去),所以O′C=
(负值舍去),所以O′C=![]()
∴OC=OB+BC=1+![]() =
=![]() ,∴点O′的坐标为(
,∴点O′的坐标为(![]() ,
,![]() ).
).


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】在实数范围内定义运算“♀”,该运算同时满足下列条件:
(1)x♀x=5,(x≠5);(2)x♀(y♀z)=(x♀y)+z,则2015♀2017的值是( )
A. 2 B. 3 C. 2015 D. 2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一小球以15 m/s的速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系h=15t-5t2,则小球经过____s达到10 m高.
查看答案和解析>>
科目:初中数学 来源: 题型:
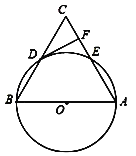
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
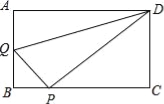

(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 三视图是中心投影
B. 小华观察牡丹花,牡丹花就是视点
C. 球的三视图均是半径相等的圆
D. 阳光从矩形窗子里照射到地面上得到的光区仍是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com