
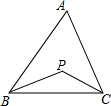
 如图,△ABC,点P是∠B、∠C的平分线交点.
如图,△ABC,点P是∠B、∠C的平分线交点.分析 (1)在△ABC内,由三角形内角和定理可求得∠ABC+∠ACB,再利用角平分线的定义可求得∠PBC+∠PCB,在△PBC中由三角形内角和可求得∠BPC;
(2)由(1)的过程可证明其正确.
解答 解:
(1)∵BP、CP为角平分线,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$×(180°-80°)=50°,
∴∠BPC=180°-(∠PBC+∠PCB)=180°-50°=130°;
(2)正确,理由如下:
∵BP、CP为角平分线,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠A)=90°-$\frac{1}{2}$∠A,
∴∠BPC=180°-(∠PBC+∠PCB)=180°-(90°-$\frac{1}{2}$∠A)=90°+$\frac{1}{2}$∠A.
点评 本题主要考查三角形内角和定理,掌握三角形内角和为180°是解题的关键,注意整体思想的应用.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
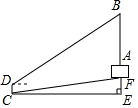 数学活动课上,老师和学生一起去侧量学校升旗台上旗杆AB的高度,如图,老师测得升旗台前斜坡FC的坡度为1:10(即EF:CE=1:10),学生吴昊站在离旗杆水平距离为27m(即CE=27m)的点C处,测得旗杆顶端B的仰角为30°,吴昊身高CD=1.6m,升旗台AF的高1.8m,请帮同学计算出旗杆AB的高度(结果精确到0.1米,$\sqrt{3}$≈1.73).
数学活动课上,老师和学生一起去侧量学校升旗台上旗杆AB的高度,如图,老师测得升旗台前斜坡FC的坡度为1:10(即EF:CE=1:10),学生吴昊站在离旗杆水平距离为27m(即CE=27m)的点C处,测得旗杆顶端B的仰角为30°,吴昊身高CD=1.6m,升旗台AF的高1.8m,请帮同学计算出旗杆AB的高度(结果精确到0.1米,$\sqrt{3}$≈1.73).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com