
已知直线y=kx-3与x轴交于点A(4,0),与y轴交于点C,抛物线 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.

(1)求此抛物线的解析式和直线的解析式;
(2)如果点P和点Q同时出发,运动时间为t(秒),试问当t为何值时,以A、P、Q为顶点的三角形与△AOC相似;
(3)在直线CA上方的抛物线上是否存在一点D,使得△ACD的面积最大.若存在,求出点D的坐标;若不存在,请说明理由.
(1)直线的解析式为y= x-3,抛物线解析式为
x-3,抛物线解析式为 ;
;
(2)①t= ,②t=
,②t= ;(3)存在,理由见解析.
;(3)存在,理由见解析.
【解析】
试题分析:(1)将A点坐标代入直线的解析式中,即可求得k的值,从而确定该直线的解析式;将A、C的坐标代入抛物线的解析式中,可求得m、n的值,从而确定抛物线的解析式.
(2)根据(1)得到的抛物线解析式,可求得点B的坐标,根据P、Q的运动速度,可用t表示出BP、CQ的长,进而可得到AQ、AP的长,然后分三种情况讨论:
①∠APQ=90°,此时PQ∥OC,可得到△APQ∽△AOC,根据相似三角形所得比例线段即可求得t的值;
②∠AQP=90°,亦可证得△APQ∽△ACO,同①的方法可求得此时t的值;
③∠PAQ=90°,显然这种情况是不成立的.
(3)过D作y轴的平行线,交直线AC于F,设出点D的横坐标,根据抛物线和直线AC的解析式可表示出D、F的纵坐标,进而可求得DF的长,以DF为底,A点横坐标的绝对值为高即可得到△ADC的面积表达式(或由△ADF、△CDF的面积和求得),由此可求出关于△ADC的面积和D点横坐标的函数关系,根据函数的性质即可求得△ADC的面积最大值及对应的D点坐标.
试题解析:
∵直线y=kx-3过点A(4,0),∴0=4k-3,解得k= .
.
∴直线的解析式为y= x-3.
x-3.
由直线y= x-3与y轴交于点C,可知C(0,-3).
x-3与y轴交于点C,可知C(0,-3).
∴ ,解得m=
,解得m= .
.
∴抛物线解析式为
(2)对于抛物线 ,
,
令y=0,则 ,解得x1=1,x2=4.
,解得x1=1,x2=4.
∴B(1,0).
∴AB=3,AO=4,OC=3,AC=5,AP=3-t,AQ=5-2t.
①若∠Q1P1A=90°,则P1Q1∥OC(如图1),

∴△AP1Q1∽△AOC.
∴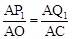 ,∴
,∴ .解得t=
.解得t= ;
;
②若∠P2Q2A=90°,∵∠P2AQ2=∠OAC,∴△AP2Q2∽△AOC.
∴ ,∴
,∴ .解得t=
.解得t= ;
;
综上所述,当t的值为 或
或 时,以P、Q、A为顶点的三角形与△AOC相似.
时,以P、Q、A为顶点的三角形与△AOC相似.
(3)答:存在.
过点D作DF⊥x轴,垂足为E,交AC于点F(如图2).

∴S△ADF=DF·AE,S△CDF=DF·OE.
∴S△ACD=S△ADF+S△CDF=DF×(AE+OE)= ×4(DE+EF)=2×(
×4(DE+EF)=2×( )=
)= .
.
∴S△ACD= (0<x<4).
(0<x<4).
又0<2<4且二次项系数 ,∴当x=2时,S△ACD的面积最大.
,∴当x=2时,S△ACD的面积最大.
而当x=2时,y= .
.
∴满足条件的D点坐标为D(2, ).
).
考点:二次函数综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 4 |
| 27 |
| 22 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com