
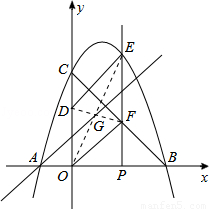
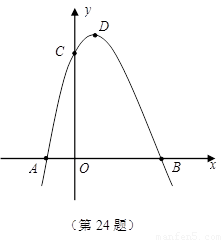
如图,抛物线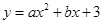 与
与 轴相交于点
轴相交于点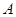 (﹣1,0)、
(﹣1,0)、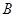 (3,0),与
(3,0),与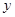 轴相交于点
轴相交于点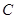 ,点
,点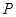 为线段
为线段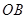 上的动点(不与
上的动点(不与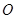 、
、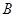 重合),过点
重合),过点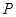 垂直于
垂直于 轴的直线与抛物线及线段
轴的直线与抛物线及线段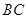 分别交于点
分别交于点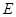 、
、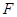 ,点
,点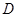 在
在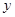 轴正半轴上,
轴正半轴上,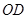 =2,连接
=2,连接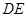 、
、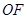 .
.
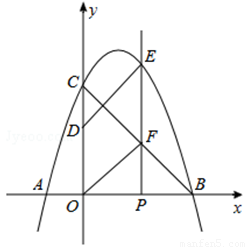
(1)求抛物线的解析式;
(2)当四边形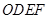 是平行四边形时,求点
是平行四边形时,求点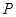 的坐标;
的坐标;
(3)过点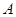 的直线将(2)中的平行四边形
的直线将(2)中的平行四边形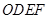 分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
(1)抛物线的解析式为: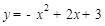 ;(2)
;(2)  点坐标为
点坐标为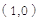 或
或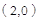 ;(3) ①当
;(3) ①当
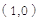 时,所求直线的解析式为:
时,所求直线的解析式为: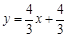 ;②当
;②当
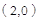 时,所求直线的解析式为:
时,所求直线的解析式为: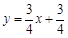 .
.
【解析】
试题分析:
(1)将点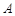 和点
和点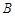 的坐标代入抛物线函数中,可求出未知量
的坐标代入抛物线函数中,可求出未知量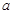 ,
,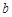 .则可求出该抛物线解析式;(2)由平行四边形的性质可知,
.则可求出该抛物线解析式;(2)由平行四边形的性质可知,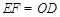 ,用含未知量
,用含未知量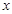 的代数式表示
的代数式表示 的长度。则可得点
的长度。则可得点 坐标
;(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点
坐标
;(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点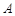 与
与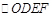 对称中心的直线平分
对称中心的直线平分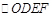 的面积.求得此直线,首先要求得
的面积.求得此直线,首先要求得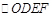 对称中心的坐标.则两点坐标可确定该直线.
对称中心的坐标.则两点坐标可确定该直线.
试题解析:
(1)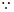 点
点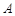
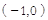 、
、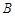
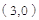 在抛物线
在抛物线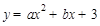 上,
上,
∴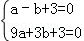 ,
,
解得 ,
,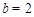 ,
,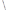 抛物线的解析式为:
抛物线的解析式为: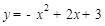 .
.
(2)在抛物线解析式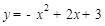 中,令
中,令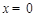 ,得
,得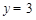 ,
,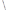
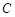
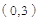 .
.
设直线BC的解析式为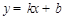 ,将
,将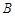
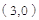 ,
,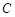
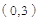 坐标代入得:
坐标代入得:
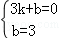 ,解得
,解得 ,
,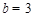 ,∴
,∴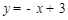 .
.
设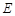 点坐标为
点坐标为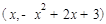 ,则
,则
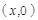 ,
,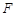
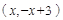 ,
,
∴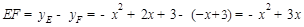
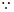 四边形
四边形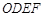 是平行四边形,
是平行四边形,
∴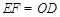 ,
,
∴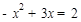 ,即
,即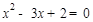 ,
,
解得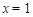 或
或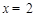 ,
,
∴ 点坐标为
点坐标为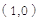 或
或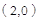 .
.
(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点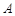 与
与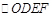 对称中心的直线平分
对称中心的直线平分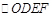 的面积.
的面积.
①当
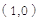 时,点
时,点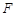 坐标为
坐标为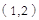 ,又
,又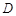
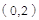
设对角线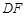 的中点为
的中点为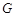 ,则
,则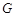
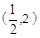 .
.
设直线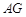 的解析式为
的解析式为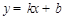 ,将
,将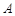
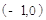 ,
,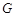
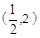 坐标代入得:
坐标代入得:
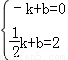 ,
,
解得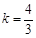 ,
,
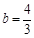 ,∴所求直线的解析式为:
,∴所求直线的解析式为: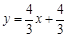 ;
;
②当
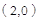 时,
时,
点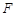 坐标为
坐标为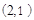 ,又
,又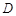
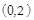 ,
,
设对角线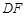 的中点为
的中点为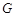 ,则
,则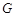
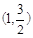 .
.
设直线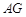 的解析式为
的解析式为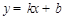 ,将
,将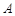
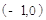 ,
,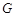
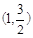 坐标代入得:
坐标代入得:
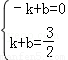 ,解得
,解得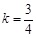 ,
,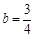 ,
,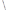 所求直线的解析式为:
所求直线的解析式为: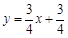 .
.
综上所述,所求直线的解析式为: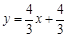 或
或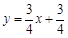 .
.
【考点】1.一次函数解析式的解法;2.二次函数解析式的解法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,抛物线与
轴相交于
、
两点(点
在点
的左侧),与
轴相交于点
,顶点为
.
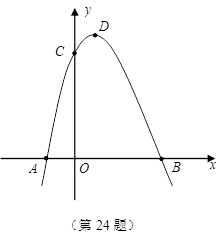
(1)直接写出、
、
三点的坐标和抛物线的对称轴;
(2)连接,与抛物线的对称轴交于点
,点
为线段
上的一个动点,过点
作
交抛物线于点
,设点
的横坐标为
;
①用含的代数式表示线段
的长,并求出当
为何值时,四边形
为平行四边形?
②设的面积为
,求
与
的函数关系式
查看答案和解析>>
科目:初中数学 来源:2012届江苏省泰兴市黄桥区九年级中考一模数学试卷(带解析) 题型:解答题
如图,抛物线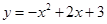 与
与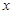 轴相交于
轴相交于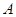 、
、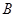 两点(点
两点(点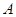 在点
在点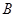 的左侧),与
的左侧),与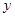 轴相交于点
轴相交于点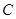 ,顶点为
,顶点为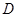 .
.
【小题1】直接写出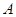 、
、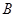 、
、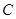 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
【小题2】连接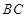 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点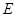 ,点
,点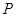 为线段
为线段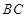 上的一个动点,过点
上的一个动点,过点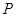 作
作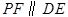 交抛物线于点
交抛物线于点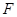 ,设点
,设点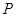 的横坐标为
的横坐标为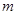 ;
;
①用含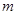 的代数式表示线段
的代数式表示线段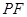 的长,并求出当
的长,并求出当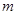 为何值时,四边形
为何值时,四边形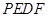 为平行四边形?
为平行四边形?
②设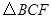 的面积为
的面积为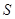 ,求
,求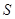 与
与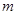 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2013届福建省泉州市洛江区初三上学期期末质量检测数学试卷(带解析) 题型:解答题
如图,抛物线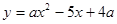 与
与 轴相交于点
轴相交于点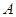 、
、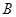 ,且经过点
,且经过点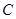 (5,4).该抛物线顶点为
(5,4).该抛物线顶点为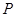 .
.
(1)求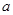 的值和该抛物线顶点
的值和该抛物线顶点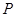 的坐标.
的坐标.
(2)求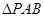 的面积;
的面积;
(3)若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省泰兴市黄桥区九年级中考一模数学试卷(解析版) 题型:解答题
如图,抛物线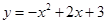 与
与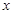 轴相交于
轴相交于 、
、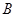 两点(点
两点(点 在点
在点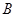 的左侧),与
的左侧),与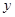 轴相交于点
轴相交于点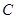 ,顶点为
,顶点为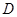 .
.

1.直接写出 、
、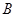 、
、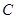 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
2.连接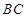 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点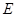 ,点
,点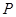 为线段
为线段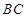 上的一个动点,过点
上的一个动点,过点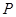 作
作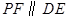 交抛物线于点
交抛物线于点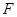 ,设点
,设点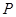 的横坐标为
的横坐标为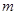 ;
;
①用含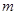 的代数式表示线段
的代数式表示线段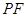 的长,并求出当
的长,并求出当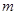 为何值时,四边形
为何值时,四边形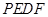 为平行四边形?
为平行四边形?
②设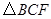 的面积为
的面积为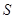 ,求
,求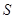 与
与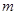 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2010-2011年重庆一中初三下学期第一次考前模拟数学试卷 题型:解答题
如图,抛物线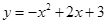 与
与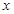 轴相交于
轴相交于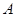 、
、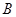 两点(点
两点(点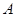 在点
在点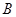 的左侧),与
的左侧),与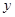 轴相交于点
轴相交于点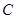 ,顶点为
,顶点为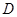 .
.
(1)直接写出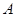 、
、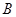 、
、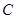 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)连接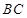 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点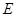 ,点
,点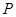 为线段
为线段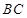 上的一个动点,过点
上的一个动点,过点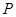 作
作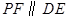 交抛物线于点
交抛物线于点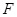 ,设点
,设点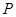 的横坐标为
的横坐标为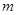 ;
;
①用含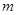 的代数式表示线段
的代数式表示线段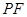 的长,并求出当
的长,并求出当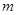 为何值时,四边形
为何值时,四边形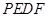 为平行四边形?
为平行四边形?
②设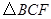 的面积为
的面积为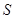 ,求
,求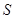 与
与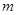 的函数关系式
的函数关系式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com