

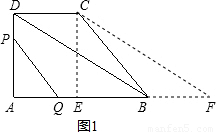
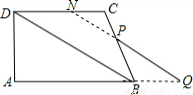
 �⣺��1����ͼ1����C����CE��AB��
�⣺��1����ͼ1����C����CE��AB��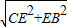 =5��
=5��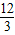 =4��
=4�� PA•AQ��
PA•AQ�� ×3t×2t=3t2��
×3t×2t=3t2�� ×AD×2t=
×AD×2t= ×4×2t=4t��
×4×2t=4t��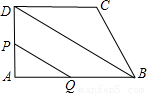
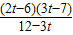 ��
�� 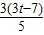 ��
��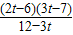 =
=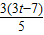 ��
��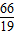 ���������⣩��
���������⣩��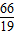 ʱ��PQ��DB��
ʱ��PQ��DB��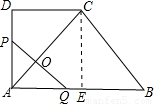 ��4������t=3
��4������t=3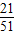 ��ʹPQ��AC���������£�
��ʹPQ��AC���������£� ʱ��P��AD�ϣ�Q��AE�ϣ���PQ��AC���ڵ�O��
ʱ��P��AD�ϣ�Q��AE�ϣ���PQ��AC���ڵ�O��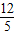 t��
t�� t��
t�� t=
t= t����t=0���˽ⲻ�������⣬���ʱPQ��AC��������
t����t=0���˽ⲻ�������⣬���ʱPQ��AC��������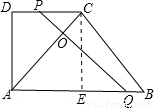 �ڵ�
�ڵ� ��t��
��t�� ʱ��P��DC�ϣ�Q��AB�ϣ���PQ��AC���ڵ�O��
ʱ��P��DC�ϣ�Q��AB�ϣ���PQ��AC���ڵ�O�� ��7-3t����
��7-3t���� t��
t�� ��7-3t��+
��7-3t��+ t=5����t=-
t=5����t=- ���˽ⲻ�������⣬���ʱPQ��AC��������
���˽ⲻ�������⣬���ʱPQ��AC��������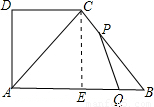 �۵�
�۵� ��t��3ʱ��P��CB�ϣ�Q��AB�ϣ�
��t��3ʱ��P��CB�ϣ�Q��AB�ϣ� BP=
BP= ��12-3t����MQ=
��12-3t����MQ= ��
��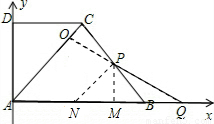 ����P��PN��OQ��AB��N����PN=BP=12-3t��BN=2BM=
����P��PN��OQ��AB��N����PN=BP=12-3t��BN=2BM= BP��
BP�� BP+��2t-6��=
BP+��2t-6��=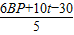 ��
��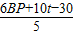 ��
��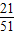 =3
=3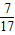 ��
��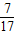 ʱ��PQ��AC��
ʱ��PQ��AC��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2011��ӱ�ʡ��̨��¡Ң��Ңɽ��ѧ�п���ѧģ���Ծ��������棩 ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011��ӱ�ʡ��̨��¡Ң��Ңɽ��ѧ�п���ѧģ���Ծ��������棩 ���ͣ������
 AB��BF=
AB��BF= BC����?ABCD�����ΪS�����ı���BEDF�����Ϊ______��
BC����?ABCD�����ΪS�����ı���BEDF�����Ϊ______�� ����̽���߶�AE��BFӦ����������������ϵ����˵�����ɣ�
����̽���߶�AE��BFӦ����������������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011��ӱ�ʡ��̨��¡Ң��Ңɽ��ѧ�п���ѧģ���Ծ��������棩 ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011��ӱ�ʡ��̨��¡Ң��Ңɽ��ѧ�п���ѧģ���Ծ��������棩 ���ͣ�ѡ����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com