
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.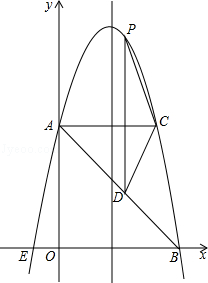
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
【答案】
(1)
解:设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5
(2)
解:当y=0时,﹣x2+4x+5=0,
∴x1=﹣1,x2=5,
∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=﹣1,n=5,
∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),
∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,
∵AC=4,
∴S四边形APCD= ![]() ×AC×PD=2(﹣x2+5x)=﹣2x2+10x,
×AC×PD=2(﹣x2+5x)=﹣2x2+10x,
∴当x=﹣ ![]() =
= ![]() 时,
时,
∴即:点P( ![]() ,
, ![]() )时,S四边形APCD最大=
)时,S四边形APCD最大= ![]()
(3)
解:如图,
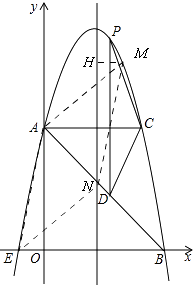
过M作MH垂直于对称轴,垂足为H,
∵MN∥AE,MN=AE,
∴△HMN≌△AOE,
∴HM=OE=1,
∴M点的横坐标为x=3或x=1,
当x=1时,M点纵坐标为8,
当x=3时,M点纵坐标为8,
∴M点的坐标为M1(1,8)或M2(3,8),
∵A(0,5),E(﹣1,0),
∴直线AE解析式为y=5x+5,
∵MN∥AE,
∴MN的解析式为y=5x+b,
∵点N在抛物线对称轴x=2上,
∴N(2,10+b),
∵AE2=OA2+OE2=26
∵MN=AE
∴MN2=AE2,
∴MN2=(2﹣1)2+[8﹣(10+b)]2=1+(b+2)2
∵M点的坐标为M1(1,8)或M2(3,8),
∴点M1,M2关于抛物线对称轴x=2对称,
∵点N在抛物线对称轴上,
∴M1N=M2N,
∴1+(b+2)2=26,
∴b=3,或b=﹣7,
∴10+b=13或10+b=3
∴当M点的坐标为(1,8)时,N点坐标为(2,13),
当M点的坐标为(3,8)时,N点坐标为(2,3)
【解析】(1)设出抛物线解析式,用待定系数法求解即可;(2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立函数关系式S四边形APCD=﹣2x2+10x,根据二次函数求出极值;(3)先判断出△HMN≌△AOE,求出M点的横坐标,从而求出点M,N的坐标.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足 ![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4. 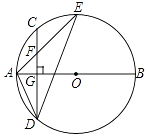
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求tan∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
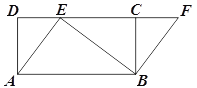
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
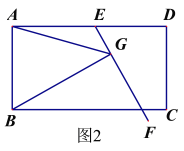
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ![]() ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 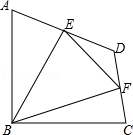
A.2
B.![]()
C.![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,AD=DC,∠DAB=∠ACB=90°,过点D作DF⊥AC,垂足为F.DF与AB相交于E.设AB=15,BC=9,P是射线DF上的动点.当△BCP的周长最小时,DP的长为 . 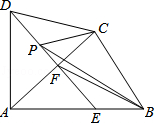
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D,F在x轴上,点C在DE边上,反比例函数y= ![]() (k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )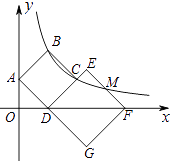
A.![]()
B.![]()
C.16
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.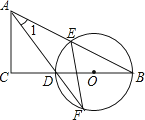
(1)求证:∠1=∠F.
(2)若sinB= ![]() ,EF=2
,EF=2 ![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com