
 )(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.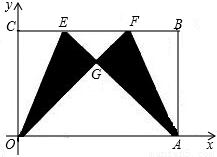
 ,而OA=BC=m,那么在直角三角形OGA中即可用勾股定理求出m的值.
,而OA=BC=m,那么在直角三角形OGA中即可用勾股定理求出m的值. ,因此P点的坐标为(1,1+
,因此P点的坐标为(1,1+ ),(1,1-
),(1,1- ).(在G点上下各有一点)
).(在G点上下各有一点)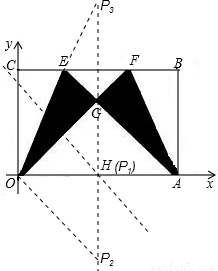
 ),
),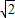 ,OG=OC=
,OG=OC=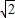 ,OA=m(2分)
,OA=m(2分)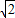 ),
),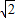 ,OG=OC=
,OG=OC=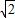 ,OA=m
,OA=m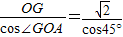 =2.
=2. 则OH=1,HG=1,故G(1,1).
则OH=1,HG=1,故G(1,1).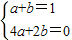 ,
, ,
, ),(1,1+
),(1,1+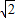 ).
).

科目:初中数学 来源:2009年浙江省绍兴市绍兴县兰亭镇中数学中考模拟试卷(解析版) 题型:解答题
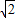 )(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.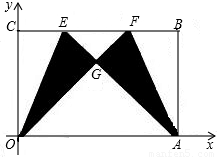
查看答案和解析>>
科目:初中数学 来源:2009年湖北省咸宁市通城县中考数学模拟试卷(解析版) 题型:解答题
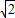 )(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.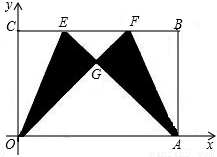
查看答案和解析>>
科目:初中数学 来源:2009年广东省茂名十中初中数学综合练习试卷(6)(解析版) 题型:解答题
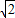 )(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
查看答案和解析>>
科目:初中数学 来源:2008年福建省南平市中考数学试卷(解析版) 题型:解答题
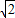 )(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.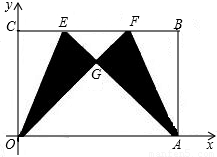
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com