
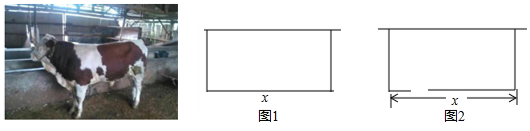
分析 (1)根据题意用含x的代数式表示出饲养室的宽,由矩形的面积=长×宽计算,再根据二次函数的性质分析即可;
(2)根据题意用含x的代数式表示出饲养室的宽,由矩形的面积=长×宽计算,再根据二次函数的性质分析即可.
解答 解:(1)∵y=x•$\frac{50-x}{2}$=-$\frac{1}{2}$(x-25)2+$\frac{625}{2}$,
∴当x=25时,占地面积最大,
即饲养室长x为25m时,占地面积y最大;
(2)∵y=x•$\frac{50-(x-2)}{2}$=-$\frac{1}{2}$(x-26)2+338,
∴当x=26时,占地面积最大,
即饲养室长x为26m时,占地面积y最大;
∵26-25=1≠2,
∴小敏的说法不正确.
点评 此题主要考查了由实际问题列二次函数关系式以及二次函数的最值问题,同时也利用了矩形的性质,解题时首先正确了解题意,然后根据题意列出方程即可解决问题.


科目:初中数学 来源: 题型:解答题
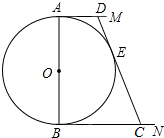 如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.
如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
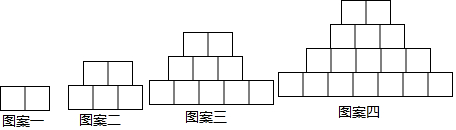
| A. | 902 | B. | 901 | C. | 900 | D. | 899 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(元/件) | 10 | 12 | 14 | 16 |
| y(件) | 200 | 180 | 160 | 140 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,港口B在港口A的正东方向,一艘船从港口A出发,沿北偏东75°方向航行20海里到C处,此时测得港口B在C的南偏东45°方向,求C到港口B的距离,(结果保留到0.01海里)(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,港口B在港口A的正东方向,一艘船从港口A出发,沿北偏东75°方向航行20海里到C处,此时测得港口B在C的南偏东45°方向,求C到港口B的距离,(结果保留到0.01海里)(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
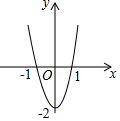 将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是( )
将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是( )| A. | y=(x-1)2+1 | B. | y=(x+1)2+1 | C. | y=2(x-1)2+1 | D. | y=2(x+1)2+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com