
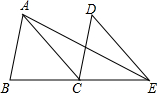
 如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( )
如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
分析 首先根据平移的性质,可得BC=CE;然后根据两个三角形的高相等时,面积和底成正比,可得△ACE的面积等于△ABC的面积,据此解答即可.
解答 解:∵将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,
∴BC=CE,
∴△ACE的面积等于△ABC的面积,
又∵△ABC的面积为2,
∴△ACE的面积为2.
故选:A.
点评 (1)此题主要考查了平移的性质和应用,要熟练掌握,解答此题的关键是要明确:①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.②新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
(2)此题还考查了三角形的面积的求法,要熟练掌握,解答此题的关键是要明确:两个三角形的高相等时,面积和底成正比.


科目:初中数学 来源: 题型:解答题
 定义{A,B,C}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x-3的“特征数”是{1,-2,-3},函数y=2x+4的“特征数”是{0,2,4},函数y=-x的“特征数”是{0,-1,0}.
定义{A,B,C}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x-3的“特征数”是{1,-2,-3},函数y=2x+4的“特征数”是{0,2,4},函数y=-x的“特征数”是{0,-1,0}.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 江阴市明天将有20%的地区降水 | B. | 江阴市明天将有20%的时间降水 | ||
| C. | 江阴市明天降水的可能性较小 | D. | 江阴市明天肯定不降水 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
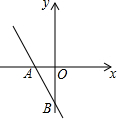 如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )
如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )| A. | m>2 | B. | m<2 | C. | m>0 | D. | m<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$$\sqrt{2}$)2=1 | B. | $\sqrt{(-6)^{2}}$=6 | C. | $\sqrt{{5}^{2}}$=±5 | D. | (3$\sqrt{2}$)2=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
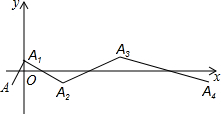 如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第11次运动后,动点A11的坐标是(120,1).
如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第11次运动后,动点A11的坐标是(120,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.
如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com