
 如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧
如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧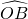 上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.
上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.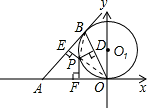 (1)证明:连接PB,OP,
(1)证明:连接PB,OP,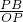 =
=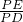 ,
,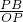 =
=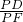 ,
,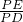 =
=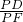 ,
, a,OD=
a,OD= a,
a, OD=
OD= a,
a, DM=
DM= a,
a, a,
a, a),
a), OP=
OP= a,OF=
a,OF= a,
a, a,
a, ),F(-
),F(- a,0),
a,0), a,BE=
a,BE= a,
a, a+a=
a+a= a,
a, OE=
OE= a,OM=
a,OM= a,
a, a,
a, a),
a), a,
a, a),D(-
a),D(- a,
a, a),
a), a-(-
a-(- a)=
a)= a,
a, a,
a, ×
× a×
a× a=
a= a2.
a2. a,
a, a),E(-
a),E(- a,
a, a),F(-
a),F(- a,0),P(-
a,0),P(- a,
a, );S△DEF=
);S△DEF= a2.
a2.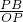 =
=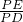 ,同理,△OPF∽△BPD,得出
,同理,△OPF∽△BPD,得出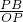 =
=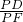 ,然后利用等量代换即可.
,然后利用等量代换即可.

科目:初中数学 来源: 题型:
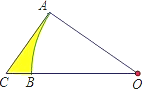 如图,OAB是以6cm为半径的扇形,AC切弧AB于点A交OB的延长线于点C,如果弧AB的长等于3cm,AC=4cm,则图中阴影部分的面积为( )
如图,OAB是以6cm为半径的扇形,AC切弧AB于点A交OB的延长线于点C,如果弧AB的长等于3cm,AC=4cm,则图中阴影部分的面积为( )| A、15cm2 | B、6cm2 | C、4cm2 | D、3cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
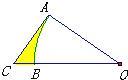 13、如图,OAB是以12cm为半径的扇形,AC切弧AB于点A交OB的延长线于点C,如果弧AB的长等于6cm,AC=8cm.则图中阴影部分的面积为
13、如图,OAB是以12cm为半径的扇形,AC切弧AB于点A交OB的延长线于点C,如果弧AB的长等于6cm,AC=8cm.则图中阴影部分的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
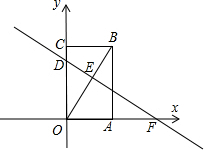 如图,OB是矩形OABC的对角线,抛物线y=-
如图,OB是矩形OABC的对角线,抛物线y=-| 1 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com