
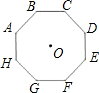
 在正八边形的8个顶点和中心O处放上9个不同的自然数,使得位于每对平行边与中心O上的5个数之和都等于位于顶点的8个数之和.那么位于中心O处的数最小是________.
在正八边形的8个顶点和中心O处放上9个不同的自然数,使得位于每对平行边与中心O上的5个数之和都等于位于顶点的8个数之和.那么位于中心O处的数最小是________. 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
 10、如图是对称中心为点O的正八边形.如果用一个含45°角的直角三角板的角,借助点O(使角的顶点落在点O处)把这个正八边形的面积n等分.那么n的所有可能的值有( )
10、如图是对称中心为点O的正八边形.如果用一个含45°角的直角三角板的角,借助点O(使角的顶点落在点O处)把这个正八边形的面积n等分.那么n的所有可能的值有( )查看答案和解析>>
科目:初中数学 来源: 题型:
 在正八边形的8个顶点和中心O处放上9个不同的自然数,使得位于每对平行边与中心O上的5个数之和都等于位于顶点的8个数之和.那么位于中心O处的数最小是
在正八边形的8个顶点和中心O处放上9个不同的自然数,使得位于每对平行边与中心O上的5个数之和都等于位于顶点的8个数之和.那么位于中心O处的数最小是查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com