
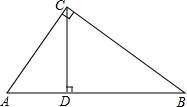
 如图,△ABC为直角三角形,∠ACB=90°,CD为斜边AB上的高,D为垂足,△ABC∽△ACD∽△CBD,那么下列等式:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④AC•CB=BA•CD,其中正确的有①②③④.(填序号)
如图,△ABC为直角三角形,∠ACB=90°,CD为斜边AB上的高,D为垂足,△ABC∽△ACD∽△CBD,那么下列等式:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④AC•CB=BA•CD,其中正确的有①②③④.(填序号) 分析 由△ABC∽△ACD∽△CBD,根据相似三角形的对应边成比例以及面积法即可求得答案.
解答 证明:∵△ABC∽△ACD,
∴$\frac{AC}{AD}$=$\frac{AB}{AC}$,
∴AC2=AD•AB.
∵△ABC∽△CBD,
∴$\frac{BC}{BD}$=$\frac{AB}{BC}$,
∴BC2=BD•BA.
∵△ACD∽△CBD,
∴$\frac{CD}{BD}$=$\frac{AD}{CD}$,
∴CD2=AD•DB,
∵在△ABC中,∠ACB=90°,CD⊥AB,
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
即∴AC•BC=AB•CD,
故①②③④正确,
故答案为①②③④.
点评 此题考查了相似三角形的判定与性质,三角形的面积,解题的关键是灵活运用相似三角形的性质解决问题,学会利用面积法证明线段之间的关系,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
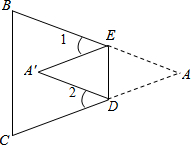 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有最小的负整数,有最大的正整数 | B. | 有最小的负数,没有最大的正数 | ||
| C. | 有最大的负数,没有最大的正数 | D. | 没有最大的有理数和最小的有理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
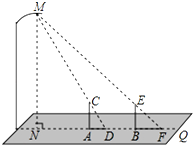 晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小军正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小聪正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高BE为1.74米,MN⊥NQ,AC⊥NQ,BE⊥NQ,请你根据以上信息,求出小军身高AC的长(结果精确到0.01米)
晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小军正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小聪正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高BE为1.74米,MN⊥NQ,AC⊥NQ,BE⊥NQ,请你根据以上信息,求出小军身高AC的长(结果精确到0.01米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
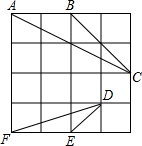 在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com