
| A. | 100 | B. | 200 | C. | 300 | D. | 400 |
分析 通过有理数的计算可得出分子=$\frac{1}{101}$+$\frac{1}{102}$+…+$\frac{1}{200}$、分母=$\frac{1}{400}$($\frac{1}{101}$+$\frac{1}{102}$+…+$\frac{1}{200}$),将其代入原分式中即可得出结论.
解答 解:分子=1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{199}$-$\frac{1}{200}$,
=1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{200}$-2×($\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{200}$),
=1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{200}$-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{100}$),
=$\frac{1}{101}$+$\frac{1}{102}$+…+$\frac{1}{200}$;
分母=$\frac{1}{(201+1)(201-1)}$+$\frac{1}{(202+2)(202-2)}$+…+$\frac{1}{(300+100)(300-100)}$,
=$\frac{1}{200×202}$+$\frac{1}{200×204}$+…+$\frac{1}{200×400}$,
=$\frac{1}{400}$($\frac{1}{101}$+$\frac{1}{102}$+…+$\frac{1}{200}$).
∴原式=$\frac{分子}{分母}$=$\frac{1}{\frac{1}{400}}$=400.
故选D.
点评 本题考查了有理数的混合运算以及规律型中数字的变化类,通过有理数的混合运算找出分子、分母间的关系是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
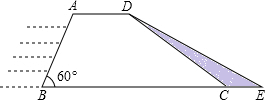 水利部门决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为4米,∠B=60°,背水坡面CD的长为4$\sqrt{3}$米,加固后大坝的横截面积为梯形ABED,CE的长为2米.
水利部门决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为4米,∠B=60°,背水坡面CD的长为4$\sqrt{3}$米,加固后大坝的横截面积为梯形ABED,CE的长为2米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
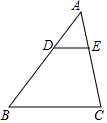 如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )
如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
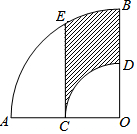 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )| A. | $\frac{4π-3\sqrt{3}}{4}$ | B. | $\frac{π-\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$+$\frac{π}{12}$ | D. | $\frac{π-3\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com