
已知一次函数y1=2x,二次函数y2=x2+1.
(Ⅰ)根据表中给出的x的值,计算对应的函数值y1,y2,并填在表格中:
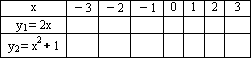
(Ⅱ)观察第(Ⅰ)问表中有关的数据,证明如下结论;在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1≤y2均成立;
(Ⅲ)试问,是否存在二次函数y3=ax2+bx+c,其图象经过点(-5,2),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值y1≤y3≤y2均成立,若存在,求出函数y3的解析式;若不存在,请说明理由.
|
解:(Ⅰ)填表如下:
(Ⅱ)证明:∵y1-y2=2x-(x2+1) =-x2+2x-1 =-(x-1)2≤0 ∴当自变量x取任意实数时,y1≤y2均成立. (Ⅲ)解:由已知,二次函数y3=ax2+bx+c的图象经过点(-5,2),得 25a-5b+c=0. ① ∵当x=1时,y1=y2=2,y3=a+b+c, 若对于自变量x取任意实数时,y1≤y3≤y2成立,则有2≤a+b+c≤2, ∴a+b+c=2. ② 由①②,得b=4a,c=2-5a, ∴y3=ax2+4ax+(2-5a). 当y1≤y3时,有 2x≤ax2+4ax+(2-5a), 即ax2+(4a-2)x+(2-5a)≥0, 若二次函数y=ax2+(4a-2)x+(2-5a)对于一切实数x,函数值大于或等于零,必须
思路点拨:(Ⅰ)根据函数的对应关系通过计算,得出结果,直接填表. (Ⅱ)只须证明对于任意的x∈R,y1≤y2恒成立即可. (Ⅲ)由y1≤y3≤y2及(Ⅰ)表知y1,y2,y3均须通过点(1,2). 这样y3的图象通过两点(1,2)及(-5,2),从而可得出两个关于a、b、c的关系式.于是b、c均可用a的代数式表示出来.再由不等式组y1≤y3≤y2确定a的值,从而可使问题获解. 评注:问题(Ⅲ)是利用已知条件和隐含条件求二次函数解析式问题,隐含条件y1,y2,y3均通过点(1,2)的挖掘是解决问题的关键.事实上,如果将y1=2x及y2=x2+1的图象画出,y1与y2必须有一个公共点(1,2),而满足y1≤y3≤y3应也必通过这一点,从而可使问题的获解心中有数(如下图).
|


科目:初中数学 来源: 题型:

| A.x<-1或0<x<3 | B.-1<x<0或x>3 |
| C.-1<x<0 | D.x>3 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年山东省济宁地区第一学期八年级期末考试数学试卷(带解析) 题型:填空题
如图,已知一次函数y1=-x+b的图象与y轴交于点A(0,4), y2=kx-2的图象与x轴交于点B(1,0).那么使y1>y2成立的自变量x的取值范围是 .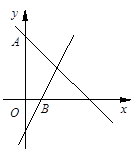
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖北黄石卷)数学 题型:选择题
已知一次函数y1=kx+b与反比例函数 在同一直角坐标系中的图象如图
在同一直角坐标系中的图象如图
所示,则当y1<y2时,x的取值范围是【 】
A.x<-1或0<x<3 B.-1<x<0或x>3
C.-1<x<0 D.x>3

查看答案和解析>>
科目:初中数学 来源:2010-2011年山东肥城马埠中学初三模拟试题三数学卷 题型:选择题
已知一次函数y1=kx+b与反比例函数y2=在同一直角坐标系中的图象如图所示,则当y1<y2时,x的取值范围是【 】
A.x<-1或0<x<3 B.-1<x<0或x>3
C.-1<x<0 D.x>3

查看答案和解析>>
科目:初中数学 来源:2010--2011学年山东肥城马埠中学初三月考模拟考试数学卷(三). 题型:选择题
已知一次函数y1=kx+b与反比例函数y2=在同一直角坐标系中的图象如图所示,则当y1<y2时,x的取值范围是【 】

A.x<-1或0<x<3 B.-1<x<0或x>3
C.-1<x<0 D.x>3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com