
判断下列问题中的两个量是否是反比例函数关系.
(1)正方形的周长l与边长a的关系.
( )
(2)正方形的面积S与边长a的关系.
( )
(3)三角形的一边a为常数,其面积S与这边上的高h的关系.
( )
(4)三角形的面积S为常数,其一边a和这边上的高h的关系.
( )
(5)时间t一定,路程s与速度v的关系.
( )
(6)路程s一定,速度v与时间t的关系.
( )
(7)某乡粮食产量为m吨,那么该乡人均拥有粮食y(吨)与人口数x(人)之间的关系.
( )
(8)功W为常数时,力F与物体在力的方向上通过的距离s的关系.
( )
|
解:是反比例函数的关系的是: (4)、(6)、(7)、(8)说明:判断两个量之间的函数关系:可先写出关系式,然后再判断如(7)、(8)、(2),写出关系式后,再根据关系式中的量的关系,确定是什么函数,如本例中的(3)、(4),虽然关系式一样,但问题不一样,在(3)中a是常数,S是h的正比例函数,在(4)中S是常数,ah=2S,即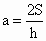 或 或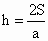 ,a与h是反比例关系.要判断两个量之间是否是反比例函数的关系,可先写出关系式,再进行判断. ,a与h是反比例关系.要判断两个量之间是否是反比例函数的关系,可先写出关系式,再进行判断.
(1)l=4a (2) (3) (4) (5)s=vt(t 为常数)(6)s=vt(s 为常数)(7) (8) |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| x | 1 | 2 | 3 | 4 | 12 | |
| y | 12.03 | 5.98 | 3.03 | 1.99 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 | 12 | |
| y | 12.03 | 5.98 | 3.03 | 1.99 | 1.00 |
查看答案和解析>>
科目:初中数学 来源:《1.3 反比例函数的应用》2010年同步练习2(解析版) 题型:解答题
| x | 1 | 2 | 3 | 4 | 12 | |
| y | 12.03 | 5.98 | 3.03 | 1.99 | 1.00 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x | 1 | 2 | 3 | 4 | 12 | |
| y | 12.03 | 5.98 | 3.03 | 1.99 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com