
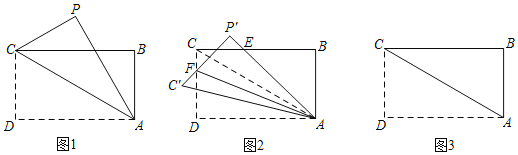
【题目】如图1,在矩形纸片![]() 中,
中,![]() ,
,![]() ,将纸片沿对角线
,将纸片沿对角线![]() 对折,点
对折,点![]() 落在点
落在点![]() 处.
处.
(1)![]() 的大小是 ;
的大小是 ;
(2)如图2,将折叠后的纸片沿着![]() 剪开,把
剪开,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 角(
角(![]() ),得到
),得到![]() ,点
,点![]() 分别对应点
分别对应点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
①当![]() 时,求证:
时,求证:![]() ;
;
②当点![]() 落在边
落在边![]() 上时,连接
上时,连接![]() ,则
,则![]() 的值为 ;
的值为 ;
③在②的条件下,将![]() 沿
沿![]() 折叠至
折叠至![]() 处,点
处,点![]() 对应点
对应点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则线段
,则线段![]() 的长度为 .
的长度为 .
科目:初中数学 来源: 题型:
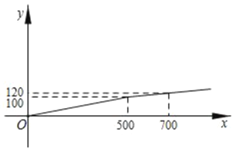
【题目】某校一课外小组准备进行“绿色环保”的宣传活动,需要印刷一批宣传单,学校附近有甲、乙两家印刷社,甲印刷社收费y(元)与印数x(张)的函数关系是:y=0.15x;乙印刷社收费y(元)与印数x(张)的函数关系如图所示:
(1)写出乙印刷社的收费y(元)与印数x(张)之间的函数关系式;
(2)若该小组在甲、乙两印刷社打印了相同数量的宣传单共用去70元,则共打印多少张宣传单?
(3)活动结束后,市民反映良好,兴趣小组决定再加印1500张宣传单,若在甲、乙印刷社中选一家,兴趣小组应选择哪家印刷社比较划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外体育活动,决定开展:篮球、乒乓球、踢毽子、跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种).随机抽取了部分学生进行调查,并将调查结果绘成如下统计图,请你结合图中信息解答下列问题.
(1)样本中最喜欢篮球项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
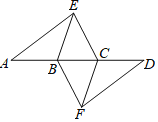
【题目】如图,点A、B、C、D依次在同一条直线上,点E、F分别在直线AD的两侧,已知BE∥CF,∠A=∠D,AE=DF.
(1)求证:四边形BFCE是平行四边形;
(2)填空:若AD=7,AB=2.5,∠EBD=60°,当四边形BFCE是菱形时,菱形BFCE的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
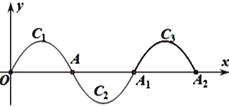
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.
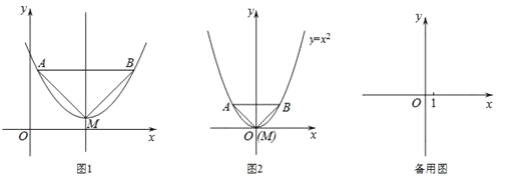
(1)①如图2,求出抛物线y=x2的“完美三角形”斜边AB的长;
②请写出一个抛物线的解析式,使它的完美三角形与y=x2+1的“完美三角形”全等;
(2)若抛物线y=ax2+4的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线y=mx2+2x+n5的“完美三角形”斜边长为n,且y=mx2+2x+n5的最大值为1,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
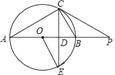
【题目】如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com