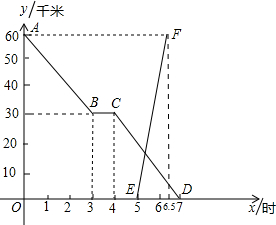
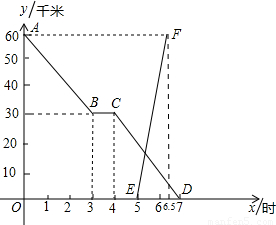
解:(1)由图象得:
小亮骑自行车的速度是:30÷3=10km/时,
小明骑摩托车的速度是:60÷1.5=40km/时;
故答案为:10,40
(2)当0≤x<3时,设小亮距乙地点的距离y与时间x之间的函数关系式为y=k
1x+b
1,由图象得:
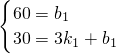
,
解得:
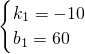
,
解析式为:y=-10x+60,(0≤x<3),
当3≤x<4时,小亮距乙地点的距离y与时间x之间的函数关系式为:
y=30,(3≤x<4)
当4≤x≤7时,设小亮距乙地点的距离y与时间x之间的函数关系式为y=k
2x+b
2,由图象得:
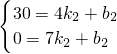
,
解得:
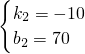
,
解析式为:y=-10x+70,(4≤x≤7);
(3)设小明距甲地的距离y与出发时间x的函数关系式为y=k
3x+b
3,由图象,得
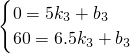
,
解得:
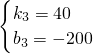
,
∴解析式为:y=40x-200,(5≤x≤6.5).
当-10x+70-(40x-200)=10时,
解得:x=5.2,
当40x-200-(-10x+70)=10时,
解得:x=5.6,
答:小亮出发5.2小时或5.6小时时与小明相距10千米.
分析:(1)通过观察图象可以看出小亮骑自行车3小时行驶了30km,小明1.5小时行驶了60km,由速度等于路程除以时间可以得出结论;
(2)设小亮距乙地点的距离y与时间x之间的函数关系式为y=kx+b,根据图象可以得出结论;
(3)先求出小明距甲地的距离y与出发时间x的函数关系式,再与小亮距乙地的关系式建立方程就可以求出其解.
点评:本题考查了路程=速度×时间的关系式的运用,待定系数法求一次函数的解析式的运用及一次函数与一元一次方程的关系式的运用,解答本题时求出解析式是关键.


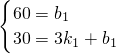 ,
,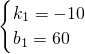 ,
,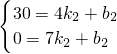 ,
,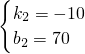 ,
,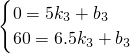 ,
,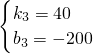 ,
,

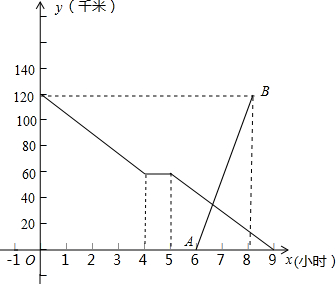 ,他距乙地的距离与时间的关系如图中线段AB所示.
,他距乙地的距离与时间的关系如图中线段AB所示.