
 23、将1~7这五个自然数填入圆锥体中各圆圈内,使三条线段上三数之和、两圆周上三数之和都等于12.
23、将1~7这五个自然数填入圆锥体中各圆圈内,使三条线段上三数之和、两圆周上三数之和都等于12. 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
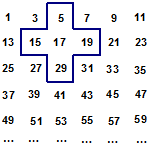 将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.
将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.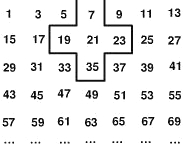
查看答案和解析>>
科目:初中数学 来源: 题型:
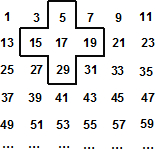 将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.
将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com