练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

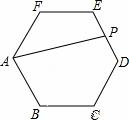
    如图，正六边形ABCDEF中，AB=2，点P是ED的中点，连接AP，则AP的长为（　　）

    A．

    B．4

    C．

    D．


    C【解析】

    试题分析：如图，连接AE，

    在正六边形中，∠F=×（6﹣2）•180°=120°。

    ∵AF=EF，∴∠AEF=∠EAF=（180°﹣120°）=30°。∴∠AEP=120°﹣30°=90°。

    ∴AE=2×2cos30°=2×2×。

    ∵点P是ED的中点，∴EP=×2=1。

    在Rt△AEP中，。

    故选C。　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知关于x的一元二次方程.

    （1）试说明：无论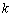取何值，方程总有两个实数根；

    （2）若△ABC的两边AB、AC的长是方程的两个实数根，第三边BC的长为5. 当△ABC是等腰三角形时，求k的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，∠AOB=90°，OA=OB，直线l经过点O，分别过A、B两点作AC⊥l交l于点C，BD⊥l交l于点D，若AC=10，BD=6，则CD=     ．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    sin60°=

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，若∠A=60°，AC=20m，则BC大约是(结果精确到0.1m)

    A．34.64m

    B．34.6m

    C．28.3m

    D．17.3m

                   

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，热气球的探测器显示，从热气球A看一栋高楼顶部B的仰角为300，看这栋高楼底部C的俯角为600，热气球A与高楼的水平距离为120m，这栋高楼BC的高度为

    A．40m　

    B．80m

    C．120m 　

    D．160m

           

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    的值是　   　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


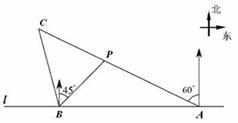
    如图，在一笔直的海岸线l上有A，B两个观测站，A在B的正东方向，AB＝2（单位：km）．有一艘小船在点P处，从A测得小船在北偏西600的方向，从B测得小船在北偏东450的方向．

    （1）求点P到海岸线l的距离；

    （2）小船从点P处沿射线AP的方向航行一段时间后，到达点C处．此时，从B测得小船在北偏西150的方向．求点C与点B之间的距离．（上述2小题的结果都保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


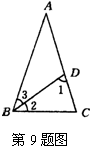
    如图所示，在△ABC中，D在AC上，连结BD，且∠ABC=∠C=∠1，∠A=∠3，则∠A 的度数为（    ）．

        A．30°    B．36°    C．45°    D．72°

     


    查看答案和解析>>

    同步练习册答案