
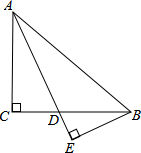
 如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,BE⊥AE,垂足为点E.求证:△BDE∽△ABE.
如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,BE⊥AE,垂足为点E.求证:△BDE∽△ABE. 分析 根据角平分线的定义,可得∠CAD与∠DAB的关系,根据对顶角相等,可得∠ADC与∠BDE的关系,根据余角的性质,可得∠DAC与∠DBE的关系,根据有两个角相等的三角形相似,可得答案.
解答 证明:∵AD是∠CAB的角平分线,
∴∠CAD=∠DAB.
∵∠ADC与∠BDE是对顶角,
∴∠ADC=∠BDE.
∵BE⊥AE,垂足为点E,
∴∠E=90°=∠C.
∵∠CAD+∠ADC=∠DBE+∠BDE,
∴∠CAD=∠DBE,
∴∠DAB=∠DBE,
又∵∠E=∠E,
∴△BDE∽△ABE.
点评 本题考查了相似三角形的判定,利用了角平分线的定义,对顶角相等,余角的性质,相似三角形的判定,利用余角的性质得出∠CAD=∠DBE是解题关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:填空题
 小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5cm,那么这张扇形纸板的面积是60πcm2.
小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5cm,那么这张扇形纸板的面积是60πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
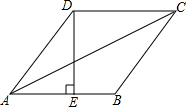 如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.
如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 质量/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| 长度/cm | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | x和y都是变量,且x是自变量,y是因变量 | |
| B. | 弹簧不悬挂重物时的长度为0 | |
| C. | 在弹性限度内,物体质量每增加1kg,弹簧长度y增加0.5cm | |
| D. | 在弹性限度内,所挂物体的质量为7kg,弹簧长度为13.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
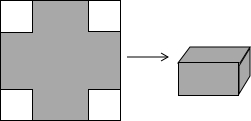 你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼成一个大正方形作为纸盒的盖.如果我们希望做成的长方体的体积为4cm3,那么用作原料的大正方形纸片的边长应是多少.
你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼成一个大正方形作为纸盒的盖.如果我们希望做成的长方体的体积为4cm3,那么用作原料的大正方形纸片的边长应是多少.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com