
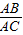 =
= ,求AC的长;
,求AC的长;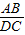 =
= ,求tanC的值.
,求tanC的值.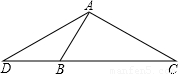
 =
= =
= ,3AD=2DC.因为DB+BC+AC=15cm.故DC+AC=15cm.AC=6cm;
,3AD=2DC.因为DB+BC+AC=15cm.故DC+AC=15cm.AC=6cm;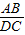 =
= ,AB=DB,故BC=2AB.DC=3AB.由(1)△DAB∽△DCA,相似比为
,AB=DB,故BC=2AB.DC=3AB.由(1)△DAB∽△DCA,相似比为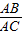 =
=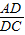 ,故AC2=3AB2.由BC=2AB,得BC2=4AB2.由勾股定理得△ABC是直角三角形.∠BAC=90度.故tanC=
,故AC2=3AB2.由BC=2AB,得BC2=4AB2.由勾股定理得△ABC是直角三角形.∠BAC=90度.故tanC=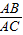 =
=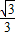 .
.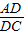 =
=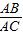 =
= .(1分)
.(1分)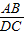 =
= ,AB=DB,
,AB=DB,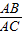 =
= .
.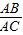 =
=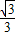 .(1分)
.(1分)

科目:初中数学 来源:2009年福建省厦门市初中学业质量检查数学试卷(解析版) 题型:解答题
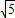 .将直线y=-3x+6绕点A旋转,记点B的对应点是B1,
.将直线y=-3x+6绕点A旋转,记点B的对应点是B1,查看答案和解析>>
科目:初中数学 来源:2009年福建省厦门市初中学业质量检查数学试卷(解析版) 题型:解答题
 x2-2x+a(x+a)=0的两个实数根为x1,x2,若y=x1+x2+
x2-2x+a(x+a)=0的两个实数根为x1,x2,若y=x1+x2+
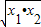 .
.查看答案和解析>>
科目:初中数学 来源:2009年福建省厦门市初中学业质量检查数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com