
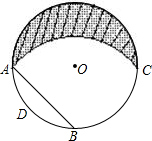
 如图,在⊙O中,
如图,在⊙O中,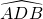 =90°,弦AB=a,以B为圆心,以BA为半径画圆弧交⊙O于另一点C,则由两条圆弧所围成的月亮形(阴影部分)的面积S=________.
=90°,弦AB=a,以B为圆心,以BA为半径画圆弧交⊙O于另一点C,则由两条圆弧所围成的月亮形(阴影部分)的面积S=________. a2
a2 a,OA=BO=
a,OA=BO= a,而S=S半圆AC-S1=S半圆AC-(S扇形BAC-S△ABC),然后根据扇形好、三角形和圆的面积公式进行计算即可.
a,而S=S半圆AC-S1=S半圆AC-(S扇形BAC-S△ABC),然后根据扇形好、三角形和圆的面积公式进行计算即可.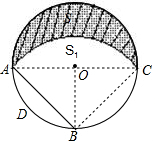 解:连OA,OB,AC,BC,如图,
解:连OA,OB,AC,BC,如图, a,OA=BO=
a,OA=BO= a,
a, π(
π( a)2-
a)2-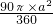 +
+ ×a×a=
×a×a= a2.
a2. a2.
a2. ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.也考查了圆心角的度数等于它所对的弧的度数和等腰直角三角形三边的关系.
lR,l为扇形的弧长,R为半径.也考查了圆心角的度数等于它所对的弧的度数和等腰直角三角形三边的关系. 

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 19、如图,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,试说明∠1=∠2,以下是证明过程,请填空:
19、如图,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,试说明∠1=∠2,以下是证明过程,请填空:查看答案和解析>>
科目:初中数学 来源: 题型:
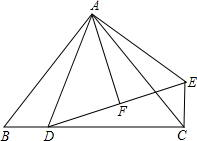 如图,在△ABC中,已知AB=AC,∠BAC=90°,D是BC上一点,EC⊥BC,EC=BD,DF=FE.求证:
如图,在△ABC中,已知AB=AC,∠BAC=90°,D是BC上一点,EC⊥BC,EC=BD,DF=FE.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
 15、如图,在△ABC中,AQ=PQ,PR=PS,PS⊥AC于S,PR⊥AB于R,则以下结论中:(1)AS=AR;(2)△BRP∽△QSP;(3)PQ∥AB中,正确的有
15、如图,在△ABC中,AQ=PQ,PR=PS,PS⊥AC于S,PR⊥AB于R,则以下结论中:(1)AS=AR;(2)△BRP∽△QSP;(3)PQ∥AB中,正确的有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com