
分析 分三种情况,根据题意画出图形,设出菱形的边长为x,再根据相似三角形的对应边成比例,列出比例式进行解答.
解答 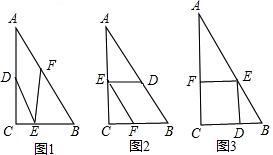 解:设Rt△ABC中,AC=4,BC=3,∠C=90°,则AB=5,
解:设Rt△ABC中,AC=4,BC=3,∠C=90°,则AB=5,
如图1,设DE=x,
∵四边形ADEF是菱形,
∴DE∥AB,
∴△CDE∽△CAB,
∴$\frac{DE}{AB}$=$\frac{CD}{CA}$,即 $\frac{x}{5}$=$\frac{4-x}{4}$,
解得x=$\frac{20}{9}$cm;
如图2,设EF=x,
由DE∥BC可知△CEF∽△CAB,
∴$\frac{EF}{AB}$=$\frac{CF}{CB}$,即$\frac{x}{5}$=$\frac{3-x}{3}$,
解得x=$\frac{15}{8}$cm;
如图3,设EF=x,
由EF∥BC可得△AEF∽△ABC,
∴$\frac{AF}{AC}$=$\frac{EF}{BC}$,即 $\frac{x}{3}$=$\frac{4-x}{4}$,
解得x=$\frac{12}{7}$cm.
故所作菱形的边长为:$\frac{20}{9}$cm、$\frac{15}{8}$cm、$\frac{12}{7}$cm.
点评 本题考查的是相似三角形的应用,解答此题的关键是根据题意画出图形,利用相似三角形的对应边成比例进行解答.解题时注意:菱形具有平行四边形的一切性质;菱形的四条边都相等.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
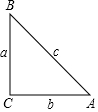 如图,在Rt△ABC中,BC,AC,AB三边的长分别为a,b,c,则sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,tanA=$\frac{a}{b}$.
如图,在Rt△ABC中,BC,AC,AB三边的长分别为a,b,c,则sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,tanA=$\frac{a}{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
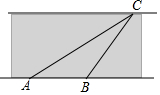 在一次数学活动课上,老师带领学生去测一条东西流向的河宽(如图所示),小明同学在河南岸点A处观测到河对岸边有一点C,测得C在点A东偏北30°方向上,沿河岸向正东前行30米到达B处,测得C在点B东偏45°的方向上,请你根据以上数据,帮助小明同学计算出这条河的宽度.
在一次数学活动课上,老师带领学生去测一条东西流向的河宽(如图所示),小明同学在河南岸点A处观测到河对岸边有一点C,测得C在点A东偏北30°方向上,沿河岸向正东前行30米到达B处,测得C在点B东偏45°的方向上,请你根据以上数据,帮助小明同学计算出这条河的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com