
已知:如图,C为半圆O上一点, AC= CE,过点C作直径AB的垂线CP,弦AE分别交PC、CB于点D、F.
(1) 求证:AD=CD;
(2) 若DF=![]() ,∠CAE=30°,求阴影部分的面积.
,∠CAE=30°,求阴影部分的面积.
 |
(1)证明:∵弧AC=弧CE
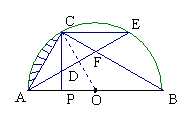 ∴ ∠CAE=∠B.
∴ ∠CAE=∠B.
∵CP⊥AB,
∴∠CPB=90°.
∴∠B+∠BCP=90°.
∵AB是直径,
∴∠ACB=90°.
∴∠ACP+∠BCP=90°
∴∠B=∠ACP.
∴∠CAE=∠ACP.
∴AD=CD.
(2)解:连结OC.
∵∠CAE=30°,
∴∠ACD=30°,∠COA=60°.
∴∠CDF=60°.
∵AB是直径,∴∠ACB=90°.
∴∠BCP=60°.
∴∠BCP=∠DCF=∠CFD=60°.
∴AD=CD=DF=![]()
∵OA=OC, ∴△AOC是等边三角形.
∴∠CAO=60°.
∴∠DAP=30°.
∵CP⊥OA,
∴AP=ADcos30°=2
∴OA=2AP=4.
∴DP=ADsin30°=![]()
∴CP=CD+DP=2![]()
∴S阴影=S扇形-S△AOC=![]() -
-![]() =
=![]()


科目:初中数学 来源: 题型:
 | BF |
 AD于点E.
AD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 点E.
点E.| 5 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 D、F.
D、F.| 4 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com