
 如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是
如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是 上的任意一点,过点C的切线分别交PA、PB于点D、E.
上的任意一点,过点C的切线分别交PA、PB于点D、E. ∠ADC;
∠ADC; ∠BEC,
∠BEC, (∠ADC+∠BEC)=110°,
(∠ADC+∠BEC)=110°,

 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
 25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.
25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.查看答案和解析>>
科目:初中数学 来源: 题型:
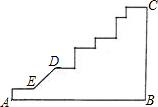 如图所示是某地地形的一部分(除D,E外每个拐角都是直角),从A到C有两条道路,一条是从A经过B再到C,另一条是从A经过E,D等地再到C.如何走近一些呢?
如图所示是某地地形的一部分(除D,E外每个拐角都是直角),从A到C有两条道路,一条是从A经过B再到C,另一条是从A经过E,D等地再到C.如何走近一些呢?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.
已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.查看答案和解析>>
科目:初中数学 来源:2010-2011学年四川省达州市渠县中学九年级(上)第二学月数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
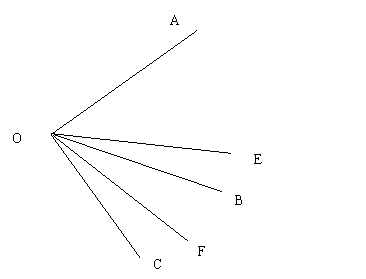
如图,OC是∠AOB外的一条射线,OE平分∠AOC,OF平分∠BOC,若∠AOC=1000,∠BOC=400,求出图中其它的角。
附加题:若∠AOB=n0,求∠EOF的度数?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com