
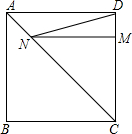
 如图所示,正方形ABCD的边长为4,点M在边DC上,且DM=1,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图所示,正方形ABCD的边长为4,点M在边DC上,且DM=1,点N是边AC上一动点,则线段DN+MN的最小值为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{17}$ | D. | 5 |
分析 如图,连接MB交AC于N,此时DN+MN最小,先证明这个最小值就是线段BM的长,利用勾股定理就是即可解决问题.
解答 解:如图,连接MB交AC于N,此时DN+MN最小.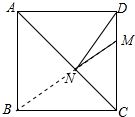
∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴DN=BN,
∴DN+MN=BN+NM=BM,
在RT△BMC中,∵∠BCM=90°,BC=4,CM=CD-DM=4-1=3,
∴BM=$\sqrt{B{C}^{2}+C{M}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
故选D.
点评 本题考查最短问题、正方形性质、勾股定理、两点之间线段最短等知识,解题的关键是利用对称找到点N的位置,属于中考常考题型.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:选择题
| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 2 | 4 | 2 | 1 |
| A. | 平均数是20.5 | B. | 众数是4 | ||
| C. | 中位数是40 | D. | 这10户家庭月用电量共205度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
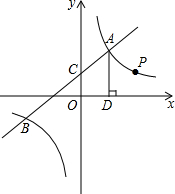 如图,一次函数y1=k1x+b 与反比例函数y2=$\frac{{k}_{2}}{x}$ 的图象交于点A(2,m)和B(-6,-2),与y轴交于点C.
如图,一次函数y1=k1x+b 与反比例函数y2=$\frac{{k}_{2}}{x}$ 的图象交于点A(2,m)和B(-6,-2),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
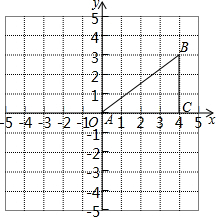 如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.
如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com