
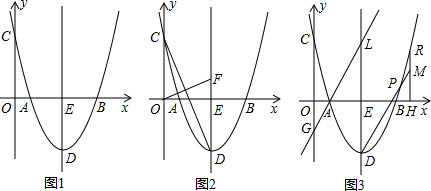
分析 (1)求出抛物线y=x2-(k+1)x+k(k>1)与x轴交点A、B的坐标,由AB=4,解关于k的方程即可;
(2)求出D、C两点坐标,线段DJ、CJ、OE用含k的代数式表示,根据等角的余切函数列比例式,求出EF的长;
(3)过点D作DN⊥RH交RH的延长线于点N,过点P作PI⊥DN交DN于点I交x轴于点S,作PQ⊥RN于点Q,过点G作GT⊥DE于点T,证明Rt△GTL∽Rt△DNM,运用等角的余切函数列比例式,求出EL的长.
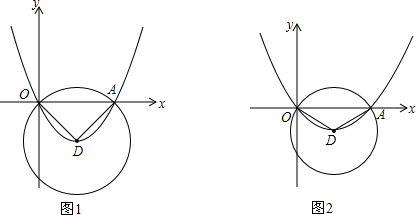
解答 解:(1)如图1,当y=0时,x2-(k+1)x+k=0,解得x=1或x=k,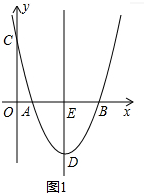
∵点A在点B的左侧,k>1,
∴A(1,0),B(k,0),
∵AB=k-1=4,
∴k=5,
∴抛物线的解析式为:y=x2-6x+5;
(2)如图1,过点D作DJ⊥y轴于点J,
∵y=x2-(k+1)x+k=(x-$\frac{k+1}{2}$)2+$\frac{-{k}^{2}+2k-1}{4}$
∴点D坐标为($\frac{k+1}{2}$,$\frac{-{k}^{2}+2k-1}{4}$),
∵∠DJO=∠JOE=∠OED=90°,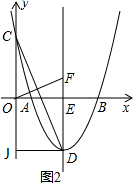
∴四边形OJDE是矩形,
∴DJ=OE=$\frac{k+1}{2}$,
∵C(0,k)
∴CJ=k-$\frac{-{k}^{2}+2k-1}{4}$=$\frac{(k+1)^{2}}{4}$,
∵∠FOE=∠COD,
∴tan∠FOE=tan∠OCD,
∴$\frac{EF}{OE}=\frac{DJ}{CJ}$
∴EF=$\frac{DJ•OE}{CJ}$=1,
∴点F的纵坐标为1;
(3)过点D作DN⊥RH交RH的延长线于点N,过点P作PI⊥DN交DN于点I交x轴于点S,作PQ⊥RN于点Q,过点G作GT⊥DE于点T,
同理可得,四边形EDNH、GTEO、PINQ均为矩形,
∵y=x2-6x+5=(x-3)2-4,
∴D(3,-4),C(0,5),
∴GT=OE=3,
∵点R与点C关于对称轴对称,
∴OH=6,
∴R(6,5)
∴DN=EH=6-3=3,
设PQ=m,PS=n,
∴P(6-m,n),
∵点P在抛物线上,
∴n=(6-m)2-6(6-m)+5=m2-6m+5,
∵PI=m2-6m+5+4=(m-3)2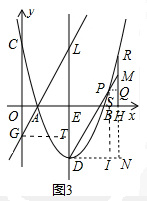 ,DI=3-m,
,DI=3-m,
∴tan∠NDM=$\frac{MN}{ND}$=tan∠PDI=$\frac{PI}{DI}$=$\frac{(m-3)^{2}}{3-m}$=3-m,
∴MN=9-3m,
∵RN=9,
∴RM=9-(9-3m)=3m,
∴MP=RM=3m,MQ=$\sqrt{M{P}^{2}-P{Q}^{2}}$=$\sqrt{(3m)^{2}-{m}^{2}}$=2$\sqrt{2}$m,
∴tan∠DMN=tan∠PMQ=$\frac{PQ}{MQ}$=$\frac{m}{2\sqrt{2}m}$=$\frac{\sqrt{2}}{4}$,
∵GL=DM,GT=DN=3,
∴Rt△GTL≌Rt△DNM,
∴∠ALE=∠DMN,
∴tan∠ALE=tan∠DMN=$\frac{\sqrt{2}}{4}$,
∵tan∠ALE=$\frac{AE}{EL}$,
∴$\frac{\sqrt{2}}{4}=\frac{2}{EL}$,
∴EL=4$\sqrt{2}$.
点评 本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式、利用三角函数解直角三角形、相似三角形的判定和性质以及解一元二次方程的问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 得分 | 80 | 85 | 87 | 90 |
| 人数 | 1 | 3 | 2 | 2 |
| A. | 85、85 | B. | 87、85 | C. | 85、86 | D. | 85、87 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
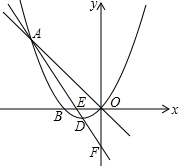 如图,已知二次函数y=ax2+bx+c(a≠0)的图象过原点O,与x轴相交于点B(-4,0),顶点为D,直线y=-x与二次函数的图象交于点A(m,8),直线AD交x轴于点E,交y轴于点F.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象过原点O,与x轴相交于点B(-4,0),顶点为D,直线y=-x与二次函数的图象交于点A(m,8),直线AD交x轴于点E,交y轴于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (π-3.14)0是无理数 | B. | $\sqrt{(-5)^{2}}=-5$ | C. | (x2)2=x5 | D. | $(-\frac{1}{4})^{-2}=16$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
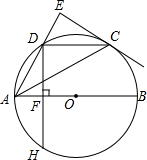 如图,AB是⊙O的直径.点C、D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF丄AB于点F,交⊙O于点H.连接DC、AC.
如图,AB是⊙O的直径.点C、D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF丄AB于点F,交⊙O于点H.连接DC、AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com