Question

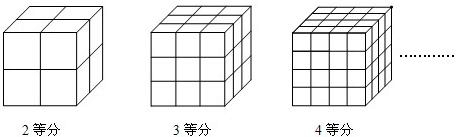
天天是一个动手能力很强的同学．他将正方体的表面全部涂上颜色．然后把正方体的每条棱2等分，再沿等分线把正方体切开，得到8个小正方体．通过观察他发现：8个小正方体全是3个面涂有颜色的．
（1）天天又把另一个正方体的棱三等分，然后沿等分线把正方体切开，得到了27个小正方体，表面涂色后，请你帮天天观察推理：这27个小正方体中，有

8

个是3个面涂有颜色的，有

12

个是2个面涂有颜色的，还有

1

个是各个面都没有涂色的．
（2）如果把正方体四等分呢？表面涂色后，有

8

个是各个面都没有涂色的．
（3）通过上面的小实验，回答下面问题：现在有一个很大的正方体（足够切），把每条棱都n等分后切开．数出各个面都没有涂色的正方体数为125，请问，n=

7

．

Answer 1

分析：（1）正方体有6个面，8个顶点，最中间露不出来的那一个面无涂色，每个面的中间一块涂色1面，8个顶点上的面三面涂色．
（2）根据正方体的性质可发现棱四等分时的所得小正方体表面涂色情况；
（3）根据已知图形中没有涂色的小正方形个数得出变化规律进而得出答案．

解答：解：（1）共有27个面，最中间露不出来的那一个面无涂色，个数为1，每个面的中间一块涂色1面，个数为6，
8个顶点上的面三面涂色，个数为8，
其余两面涂色，个数为12，
故答案为：8，12，1；

（2）由题意可得出：有8个是各个面都没有涂色的；
故答案为：8；

（3）根据正方体的棱三等分时有1个是各个面都没有涂色的，
正方体的棱四等分时有8个是各个面都没有涂色的，
∴正方体的棱n等分时有（n-2）³个是各个面都没有涂色的，
∴（n-2）³=125，
解得：n=7．
故答案为：7．

点评：本题主要考查了立体图形的认识和用特殊归纳一般规律的方法．关键是通过正方体的特点来得到有关涂色情况的规律．