解:分析所求代数式中六个绝对值的分界点,分别为:0,1,2,3,4,5.
∵x=2
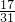
,
∴原式=|x|+|x-1|+|x-2|+|x-3|+|x-4|+|x-5|
=x+(x-1)+(x-2)-(x-3)-(x-4)-(x-5)
=-1-2+3+4+5
=9.
答:|x|+|x-1|+|x-2|+|x-3|+|x-4|+|x-5|的值为9.
分析:分析所求代数式中六个绝对值的分界点,分别为:0,1,2,3,4,5.根据绝对值的意义去掉绝对值的符号,将有3个x和3个-x,这样将抵消掉x,使求值变得容易.
原式=|x|+|x-1|+|x-2|+|x-3|+|x-4|+|x-5|=x+(x-1)+(x-2)-(x-3)-(x-4)-(x-5)=-1-2+3+4+5=9.
实际上,本题只要x的值在2与3之间,那么这个代数式的值就是9,即它与x具体的取值无关.
点评:本题主要考查根据绝对值的意义去掉绝对值的符号,以及代数式的求值问题,要认真掌握,并确保得分.

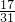 时,求代数式|x|+|x-1|+|x-2|+|x-3|+|x-4|+|x-5|的值.
时,求代数式|x|+|x-1|+|x-2|+|x-3|+|x-4|+|x-5|的值.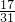 ,
,
