
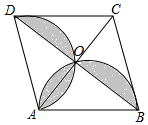
 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,分别以AB、AD为直径作一个半圆,则图中阴影部分的面积为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,分别以AB、AD为直径作一个半圆,则图中阴影部分的面积为( )| A. | $\frac{25}{4}$π-12 | B. | $\frac{16}{3}$π-3 | C. | $\frac{9}{2}$π-6 | D. | $\frac{25}{8}$π-6 |
分析 根据菱形的对角线互相垂直平分求出OA、OB,再利用勾股定理列式求出AB,然后根据阴影部分的面积的一半等于半圆的面积减去△AOB的面积,列式计算即可得解,
解答 解:∵菱形ABCD中,AC=6,BD=8,
∴AC⊥BD且OA=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,
OB=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4,
由勾股定理得,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴阴影部分的面积=[$\frac{1}{2}$•π($\frac{5}{2}$)2-$\frac{1}{2}$×4×3]×2=$\frac{25}{4}$π-12.
故选:A.
点评 本题考查了菱形的性质,勾股定理,主要利用了菱形的对角线互相垂直平分的性质,熟记性质并观察出阴影部分的面积的表示是解题的关键.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
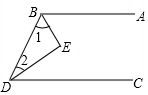 (1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.
(1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
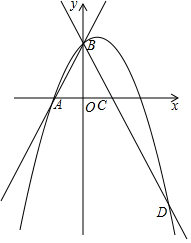 如图,直线y=2x+2与x轴交于点A,与 y轴交于点B,把△AOB沿y轴翻析,点A落到C点,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).
如图,直线y=2x+2与x轴交于点A,与 y轴交于点B,把△AOB沿y轴翻析,点A落到C点,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com