

分析 (1)先利用坐标系中坐标轴上的点的特征得出点A坐标,再用含30度角的直角三角形的性质即可得出点B坐标;
(2)先求出AD,BC得出AD=BC,再判断出AD∥BC即可得出结论;
(3)由旋转得出∠A1OB=30°,进而由含30°的直角三角形的性质即可得出结论;
(4)分两种情况利用平行四边形的性质和等边三角形的性质即可得出结论.
解答 解:(1)直线y=$\frac{\sqrt{3}}{4}$(x+1)的图象与x轴交于点A.
∴A(-1,0),
∴OA=1,
在Rt△AOB中,∠ABO=30°,
∴OB=$\sqrt{3}$,AB=2,
∴B(0,$\sqrt{3}$),
∵直线y=$\frac{\sqrt{3}}{4}$(x+1)的图象过点C(3,n),
∴n=$\sqrt{3}$,故答案为:(-1,0),(0,$\sqrt{3}$),$\sqrt{3}$,
(2)由(1)知,A(-1,0),
∵D(2,0),
∴AD=3,由(1)知,B(0,$\sqrt{3}$),
∵C(3,$\sqrt{3}$),
∴BC∥AD,BC=3,
∴AD=BC,
∴四边形ABCD是平行四边形,
(3)如图1,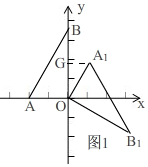 由旋转知,∠AOA1=120°,OA1=OA=1,
由旋转知,∠AOA1=120°,OA1=OA=1,
∵∠AOB=90°,
∴∠A1OB=30°,
过点A1作A1G⊥OB于G,
在Rt△A1OG中,OA1=1,
∴A1G=$\frac{1}{2}$,OG=$\frac{\sqrt{3}}{2}$,
∴A1($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
(4)①当OD为对角线时,如图2,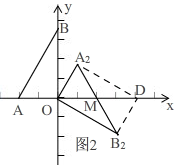 ∵四边形OA2DB2是平行四边形,
∵四边形OA2DB2是平行四边形,
∴OM=DM=1,A2M=B2M=1,
由旋转知OA2=OA=1,
∴△OA2M是等边三角形,
∴A2($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
②当OA为边时,如图3,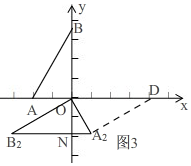 ∵四边形ODA2B2是平行四边形,
∵四边形ODA2B2是平行四边形,
∴A2B2∥OD,交y轴于N,
由旋转知,OA2=1,OB2=$\sqrt{3}$,A2B2=2,
在Rt△A2ON中,A2N=$\frac{1}{2}$,ON=$\frac{\sqrt{3}}{2}$,
∴A2($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).
点评 此题是三角形综合题,主要考查了坐标轴上点的特征,含30°角的直角三角形的性质,旋转的性质,等边三角形的判定和性质,解(2)的关键是判断出BC∥AD,解(3)的关键是求出∠A1OB=30°,解(4)的关键是分类讨论.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
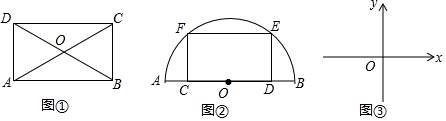
 如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.[注y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)]
如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.[注y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)]查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.166×107 | B. | 1.66×106 | C. | 16.6×105 | D. | 166×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com