解:
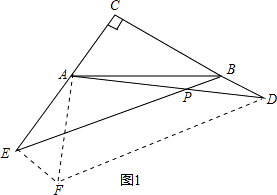
(1)作EF等于且平行BD,则EP平行FD,
∴∠APE=∠ADF,
∴△ACD≌△AEF,
∴AD=AF,
∴△AFD为等腰直角三角形.
∴∠APE=45°.
答:∠APE的度数为45°.
(2)解法一:如图2,
将AE平移到DF,连接BF,EF.
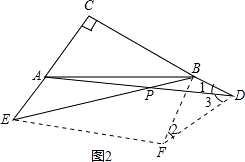
则四边形AEFD是平行四边形.
∴AD∥EF,AD=EF.
∵

,

,
∴

,

.
∴

.
∵∠C=90°,
∴∠BDF=180°-∠C=90°.
∴∠C=∠BDF.
∴△ACD∽△BDF.
∴

,∠1=∠2.
∴

.
∵∠1+∠3=90°,
∴∠2+∠3=90°.
∴BF⊥AD.
∴BF⊥EF.
∴在Rt△BEF中,

.
∴∠APE=∠BEF=30°.
解法二:如图3,将CA平移到DF,
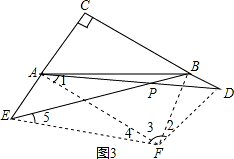
连接AF,BF,EF.
则四边形ACDF是平行四边形.
∵∠C=90°,
∴四边形ACDF是矩形,
∠AFD=∠CAF=90°,∠3+∠2=90°.
∵在Rt△AEF中,
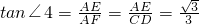
,
在Rt△BDF中,
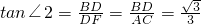
,
∴∠4=∠2=30°.
∴∠3+∠2=∠4+∠2=90°,即∠EFB=90°.
∴∠AFD=∠EFB.
又∵

,
∴△ADF∽△EBF.
∴∠1=∠5.
∵∠APE+∠1=∠4+∠5,
∴∠APE=∠4=30°.
答:∠APE的度数为30°.
分析:(1)作EF等于且平行BD,则EP平行FD,∠APE=∠ADF,可证AD=AF(全等),然后可得△AFD为等腰直角三角形.
所以∠APE=∠ADF=45°.
(2)此题有2种解法,解法一:如图2,将AE平移到DF,连接BF,EF.则四边形AEFD是平行四边形,利用已知条件求证
△ACD∽△BDF.利用其对应边成比例可得

=

,然后再利用在Rt△BEF中,

即可求得答案.
解法二:如图3,将CA平移到DF,连接AF,BF,EF.则四边形ACDF是平行四边形.根据∠C=90°,可得四边形ACDF是矩形,分别求出tan∠3和tan∠1,再利用

,求证△ADF∽△EBF利用等量代换即可求得答案.
点评:此题主要考查相似三角形的判定与性质和解直角三角形等知识点,综合性较强,有一定的拔高难度,属于难题.

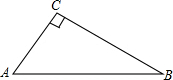 在Rt△ABC中,∠C=90°,D,E分别为CB,CA延长线上的点,BE与AD的交点为P.
在Rt△ABC中,∠C=90°,D,E分别为CB,CA延长线上的点,BE与AD的交点为P. ,
, ,求∠APE的度数.
,求∠APE的度数.

 ,
, ,
, ,
, .
. .
. ,∠1=∠2.
,∠1=∠2. .
. .
.
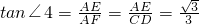 ,
,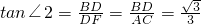 ,
, ,
, =
= ,然后再利用在Rt△BEF中,
,然后再利用在Rt△BEF中, 即可求得答案.
即可求得答案. ,求证△ADF∽△EBF利用等量代换即可求得答案.
,求证△ADF∽△EBF利用等量代换即可求得答案.
