
已知点(﹣1,y1),(2,y2),(3,y3)在反比例函数y=
 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y1>y2 D.y2>y3>y1
B【考点】反比例函数图象上点的坐标特征.
【专题】压轴题.
【分析】先判断出函数反比例函数y=
 的图象所在的象限,再根据图象在每一象限的增减性及每一象限坐标的特点进行判断即可.
的图象所在的象限,再根据图象在每一象限的增减性及每一象限坐标的特点进行判断即可.
【解答】解:∵k2≥0,∴﹣k2≤0,﹣k2﹣1<0,
∴反比例函数y=
 的图象在二、四象限,
的图象在二、四象限,
∵点(﹣1,y1)的横坐标为﹣1<0,∴此点在第二象限,y1>0;
∵(2,y2),(3,y3)的横坐标3>2>0,∴两点均在第四象限y2<0,y3<0,
∵在第四象限内y随x的增大而增大,
∴0>y3>y2,
∴y1>y3>y2.
故选:B.
【点评】本题考查了反比例函数图象上点的坐标特征:当k>0时,图象分别位于第一、三象限,横纵坐标同号;当k<0时,图象分别位于第二、四象限,横纵坐标异号.


科目:初中数学 来源: 题型:
如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C1处,BC1交AD于点E,则线段DE的长为( )

A.3 B. C.5 D.
C.5 D.
查看答案和解析>>
科目:初中数学 来源: 题型:
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
|
| 甲 | 乙 |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
小华不小心将墨水溅在同桌小丽的作业本上,结果二元一次方程组 中第一个方程y的系数和第二个方程x的系数看不到了,现在已知小丽的结果是
中第一个方程y的系数和第二个方程x的系数看不到了,现在已知小丽的结果是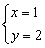 ,你能由此求出原来的方程组吗?
,你能由此求出原来的方程组吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来(如图),则这堆正方体货箱共有( )


A.4箱 B.5箱 C.6箱 D.7箱
查看答案和解析>>
科目:初中数学 来源: 题型:
某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角坐标系中,点A的坐标是(0.3),点C是x轴上的一个动点,点C在x轴上移动时,始终保持△ACP是等边三角形.当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).
(1)点C在移动的过程中,当等边三角形ACP的顶点P在第三象限时(如图),求证:△AOC≌△ABP;由此你发现什么结论?
(2)求点C在x轴上移动时,点P所在函数图象的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com